Программи́рование — процесс создания компьютерных программ.

По известному выражению Никлауса Вирта «Программы = алгоритмы + структуры данных»; иными словами, ключевыми непосредственными задачами программирования являются создание и использование алгоритмов и структур данных.

В более широком смысле под программированием понимают весь спектр деятельности, связанный с созданием и поддержанием в рабочем состоянии программ — программного обеспечения. Эта инженерно-техническая дисциплина называется «программная инженерия». Сюда входят анализ и постановка задачи, проектирование программы, построение алгоритмов, разработка структур данных, написание текстов программ, отладка и тестирование программы (испытания программы), документирование, настройка (конфигурирование), доработка и сопровождение.

Программирование основывается на использовании языков программирования, на которых записываются инструкции для компьютера. Современное приложение содержит множество таких инструкций, связанных между собой.

Текстовый редактор среды программирования может иметь специфичную функциональность, такую, как индексация имен, отображение документации, подсветка синтаксиса, средства визуального создания пользовательского интерфейса (GUI/UI). С помощью текстового редактора программист производит набор и редактирование текста создаваемой программы, который называют исходным кодом. Язык программирования определяет синтаксис и изначальную семантику исходного кода.

В настоящее время активно используются интегрированные среды разработки, включающие в свой состав также редактор для ввода и редактирования текстов программ, отладчики (т. н. дебаггеры) для поиска и устранения ошибок, трансляторы с различных языков программирования, компоновщики для сборки программы из нескольких модулей и другие служебные модули.

Антикитерский механизм из Древней Греции был калькулятором, использовавшим шестерни различных размеров и конфигурации, обусловливавших его работу, по отслеживанию метонова цикла, до сих пор использующегося в лунно-солнечных календарях.Аль-Джазари построил программируемый автомат-гуманоид в 1206 году. Одна система, задействованная в этих устройствах, использовала зажимы и кулачки, помещённые в деревянный ящик в определённых местах, которые последовательно задействовали рычаги, которые, в свою очередь, управляли ударными инструментами.

Часто первым программируемым устройством принято считать жаккардовый ткацкий станок, построенный в 1804 году Жозефом Мари Жаккаром, который произвёл революцию в ткацкой промышленности, предоставив возможность программировать узоры на тканях при помощи перфокарт.

Первое программируемое вычислительное устройство, Аналитическую машину, разработал Чарлз Бэббидж (но не смог её построить). 19 июля 1843 года графиня Ада Августа Лавлейс, дочь великого английского поэта Джорджа Байрона, как принято считать, написала первую в истории человечества программу для Аналитической машины. Эта программа решала уравнение Бернулли, выражающее закон сохранения энергии движущейся жидкости. В своей первой и единственной научной работе Ада Лавлейс рассмотрела большое число вопросов. Ряд высказанных ею общих положений (принцип экономии рабочих ячеек памяти, связь рекуррентных формул с циклическими процессами вычислений) сохранили свое принципиальное значение и для современного программирования. В материалах Бэббиджа и комментариях Лавлейс намечены такие понятия, как подпрограмма и библиотека подпрограмм, модификация команд и индексный регистр, которые стали употребляться только в 1950-х годах. Однако ни одна из программ, написанных Адой Лавлейс, никогда так и не была запущена

Большая часть работы программистов связана с написанием исходного кода, тестированием и отладкой программ на одном из языков программирования. Исходные тексты и исполняемые файлы программ являются объектами авторского права и являются интеллектуальной собственностью их авторов и правообладателей.

Различные языки программирования поддерживают различные стили программирования (парадигмы программирования). Отчасти искусство программирования состоит в том, чтобы выбрать язык программирования, наиболее полно подходящий для решения поставленной задачи. Разные языки требуют от программиста различного уровня внимания к деталям при реализации алгоритма, результатом чего часто бывает компромисс между простотой и производительностью (или междувременем программиста и временем пользователя).

Единственный язык, напрямую выполняемый ЭВМ — это машинный язык (также называемый машинным кодом и языком машинных команд). Изначально все программы писались в машинном коде, но сейчас этого практически уже не делается. Вместо этого программисты пишут исходный код на том или ином языке программирования, затем, используя компилятор, транслируют его в один или несколько этапов в машинный код, готовый к исполнению на целевом процессоре, или в промежуточное представление, которое может быть исполнено специальным интерпретатором — виртуальной машиной. Но это справедливо только для языков высокого уровня. Если требуется полный низкоуровневый контроль над системой на уровне машинных команд и отдельных ячеек памяти, программы пишут на языке ассемблера, мнемонические инструкции которого преобразуются один к одному в соответствующие инструкции машинного языка целевого процессора ЭВМ (по этой причине трансляторы с языков ассемблера получаются алгоритмически простейшими трансляторами).

В некоторых языках вместо машинного кода генерируется интерпретируемый двоичный код «виртуальной машины», также называемый байт-кодом (byte-code). Такой подход применяется в Forth, некоторых реализациях Lisp, Java, Perl, Python, языках для .NET Framework.

 Первое знакомство с Паскалем

Структура программы на Паскале. По определению стандартного Паскаля программа состоит из заголовка программы и тела программы (блока), за которым следует точка — признак конца программы. В свою очередь, блок содержит разделы описаний и раздел операторов.

Раздел операторов имеется в любой программе и является основным. Предшествующие разделы носят характер описаний и не все обязательно присутствуют в каждой программе.

В Турбо Паскале, в отличие от стандарта, возможно следующее:

• отсутствие заголовка программы;

• разделы Const, Type, Var, Label могут следовать друг за другом в любом порядке и встречаться в разделе описаний сколько угодно раз.

Примеры программ. Уже было сказано, что Паскаль разрабатывался Н. Виртом как учебный язык. Основной принцип, заложенный в нем, — это поддержка структурной методики программирования. Этот же принцип лежит в основе псевдокода, который мы здесь называем Алгоритмическим языком (АЯ). По сути дела, расхождение между АЯ и Паскалем заключается в следующем: АЯ — русскоязычный, Паскаль — англоязычный; синтаксис Паскаля определен строго и однозначно в отличие от сравнительно свободного синтаксиса АЯ.

Запись программы на Паскале похожа на английский перевод алгоритма, записанного на Алгоритмическом языке. Сравните алгоритм деления простых дробей, записанный на АЯ, с соответствующей программой на Паскале.

Здесь использовано следующее равенство:

Даже не заглядывая в учебник по Паскалю, в данной программе можно все понять. Для этого достаточно знать английский язык.

Заголовок программы начинается со слова Program (программа), за которым следует произвольное имя, придуманное программистом (division — деление). Раздел описания переменных начинается со слова Var (variables — переменные), за которым следует список переменных. Тип указывается после двоеточия словом Integer — целый. Начало и конец раздела операторов программы отмечаются словами Begin (начало) и End (конец). В конце программы обязательно ставится точка.

Ввод исходных данных с клавиатуры производится с помощью процедуры ReadLn (read line — читать строку). На клавиатуре набирают четыре числа, отделяемые друг от друга пробелами, которые отражаются строкой на экране дисплея. После набора чисел нажимают на клавишу ввода.

Операторы присваивания в Паскале записываются так же, как в АЯ. Знак умножения — * (звездочка).

Вывод результатов на экран дисплея производится с помощью процедуры WriteLn (write line — писать в строку). В рассмотренном примере два целых числа т и п выведутся в строчку, курсор на экране перейдет в начало следующей свободной строки и работа программы завершится.

Необходимо строгое соблюдение правил правописания (синтаксиса) программы. В частности, в Паскале однозначно определено назначение знаков пунктуации. Точка с запятой (;) ставится в конце заголовка программы, в конце раздела описания переменных, после каждого оператора. Перед словом End точку с запятой можно не ставить. Запятая (,) является разделителем элементов во всевозможных списках: списке переменных в разделе описания, списке вводимых и выводимых величин.

Строгий синтаксис в языке программирования необходим прежде всего для транслятора. Транслятор — это программа, которая исполняется формально. Если, допустим, разделителем в списке переменных должна быть запятая, то любой другой знак будет восприниматься как ошибка. Если точка с запятой является разделителем операторов, то транслятор в качестве оператора воспринимает всю часть текста программы от одной точки с запятой до другой. Если вы забыли поставить этот знак между какими-то двумя операторами, то транслятор будет принимать их за один, что неизбежно приведет к ошибке.

Основное назначение синтаксических правил — придать однозначный смысл языковым конструкциям. Если какая-то конструкция может трактоваться двусмысленно, значит, в ней обязательно содержится ошибка. Лучше не полагаться на интуицию, а выучить правила языка.

В дальнейшем мы строго опишем синтаксические правила Паскаля, а пока для получения первоначального представления о языке обратимся еще к нескольким примерам программирования несложных алгоритмов.

«Оттранслируем» алгоритм вычисления факториала натурального числа (N!) на Паскале.

Из этого примера, во-первых, видно, как записывается на Паскале оператор цикла с предусловием (цикл-пока):

While <условие выполнения> Do <тело цикла>

(While — пока, Do — делать). Если тело цикла содержит последовательность операторов, то говорят, что оно образует составной оператор, в начале и в конце которого надо писать Begin и End

Служебные слова Begin и End часто называют операторными скобками, которые объединяют несколько операторов в один составной. Если же тело цикла — один оператор (не составной), то операторных скобок не требуется. Тогда транслятор считает, что тело цикла заканчивается на ближайшем знаке «;».

Во-вторых, из примера видно, что в Паскале нет специальных слов для обозначения начала цикла (нц) и конца цикла (кц). На все случаи есть универсальные слова Begin и End.

Рассмотрим еще один пример программы — решение квадратного уравнения.
 

В этой программе по сравнению с предыдущими появилось много новых элементов. Имя вещественного типа в Паскале — real.

Цикл с постусловием (цикл-до) программируется оператором

Repeat <тело цикла> Until <условие окончания>

(здесь Repeat — повторять, Until — до). Тело цикла может быть как одиночным, так и составным оператором, однако употребления Begin и End не требуется, поскольку сами слова Repeat и Until выполняют роль операторных скобок.

Знак не равно в Паскале пишется так: <>, знак больше или равно: >=.

Правила записи арифметических выражений мы подробно рассмотрим немного позже. В формулах вычисления корней используется стандартная функция квадратного корня (

), которая в Паскале записывается так: sqrt (x). Порядок выполнения операций в выражении определяется скобками и старшинством операций. Старшинство операций такое же, как и в алгебре. Операции одинакового старшинства выполняются в порядке их записи (слева направо).

Ветвление в Паскале программируется с помощью условного оператора, который имеет следующую форму:

If <условие> Then <оператор 1> Else «oператор 2>

(здесь If — если, Then — то, Else — иначе). Операторы 1 и 2 могут быть как простыми, так и составными. Составной оператор следует заключать в операторные скобки Begin и End.

Так же, как и в Алгоритмическом языке, возможно использование неполной формы условного оператора:

if <условие> then <оператор>

Характерной чертой данной программы является использование в тексте комментариев. Комментарий — это любая последовательность символов, заключенных в фигурные скобки {...}. Можно употреблять также следующие ограничители комментариев (*...*). Комментарий не определяет никаких действий программы и является лишь пояснительным текстом. Он может присутствовать в любом месте программы, где можно поставить пробел

Программист пишет комментарии не для компьютера, а для себя. Комментарий придает тексту программы большую ясность. Хорошо откомментированные программы называют самодокументированными. Во многих подобных программах объем комментариев превышает объем вычислительных операторов.

Удачное использование комментариев — признак хорошего стиля программирования.

Чтобы выполнить программу на ЭВМ, ее нужно ввести в память, оттранслировать и исполнить. Для того чтобы проделать всю эту работу, на компьютере должны быть специальные средства программного обеспечения. На ПК они составляют систему Турбо Паскаль.

Упражнения

«Оттранслируйте» с Алгоритмического языка на Паскаль следующие алгоритмы:

а) алгоритм Евклида;

б) алгоритм выбора наибольшего значения из трех;

в) алгоритм определения существования треугольника с данными длинами сторон;

г) алгоритм умножения двух целых чисел с использованием только операций сложения и вычитания;

д) алгоритм вычисления частного и остатка от целочисленного деления.

Элементы языка Турбо Паскаль

Алфавит. Алфавит языка состоит из множества символов, включающих в себя буквы, цифры и специальные символы.

Латинские буквы: от A до Z (прописные) и от а до z. (строчные).

Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Шестнадцатеричные цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F.

Специальные символы: + — * / = < > [ ] . , ( ) : ; { } ^ @ $  #.

Следующие комбинации специальных символов являются едиными символами (их нельзя разделять пробелами):

: = знак присваивания;                < =   меньше или равно;

> = больше или равно;                 (* *) ограничители комментариев

< > не равно;                                 (используются наряду с {});

(..)   эквивалент [ ].

Пробелы — символ пробела (ASCI1-32) и все управляющие символы кода ASCII (от 0 до 31).

К спецсимволам относятся служебные слова, смысл которых определен однозначно. Служебные слова не могут быть использованы для других целей. С точки зрения языка это единые символы. Вот список служебных слов Турбо Паскаля:

Последние версии языка содержат еще ряд служебных слов, относящихся к работе с объектами и встроенным ассемблером.

Идентификаторы. Идентификатором называется символическое имя определенного программного объекта. Такими объектами являются имена констант, переменных, типов данных, процедур и функций, программ. С помощью синтаксической диаграммы идентификатор можно определить, как показано на рис. 8.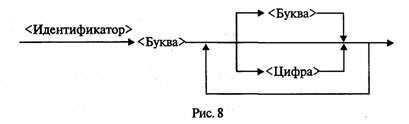

Расшифровать это можно так: идентификатор — это любая последовательность букв и цифр, начинающаяся с буквы. В Турбо Паскале к буквам приравнивается также знак подчеркивания. Строчные и прописные буквы в идентификаторах и служебных словах не различаются. Например: max, MAX, MaX и mAx — одно и то же имя.

Длина идентификатора может быть произвольной, но значащими являются только первые 63 символа.

Комментарии. Следующие конструкции представляют собой комментарии и поэтому игнорируются компилятором:

(любой текст, не содержащий символ «}» }

(* любой текст, не содержащий символы «*)»*)

Буквы русского алфавита употребляются только в комментариях, в литерных и текстовых константах.

Строка, начинающаяся с символов {$ или (*$, является директивой компилятора. За этими символами следует мнемоника команды компилятора.
 

Типы данных

Концепция типов данных является одной из центральных в любом языке программирования. С типом величины связаны три ее свойства: форма внутреннего представления, множество принимаемых значений и множество допустимых операций. Турбо Паскаль характеризуется большим разнообразием типов данных, отраженном на рис. 9.

В стандартном Паскале отсутствует строковый тип. Кроме того, в Турбо Паскале целые и вещественные — это группы типов. В старших версиях Турбо Паскаля существует процедурный тип и тип объект.

Каждый тип имеет свой идентификатор.

В табл. 3.1 представлена информация о простых типах данных, определенных в Турбо Паскале. Для вещественных типов в скобках указано количество сохраняемых значащих цифр мантиссы в десятичном представлении числа.

Таблица 3.1
 

В стандарте Паскаля из вещественных типов определен только тип Real; из целых типов — Integer.

Типы Single, Double, Extended употребляются в Паскаль-программах только в том случае, если ПК снабжен сопроцессором «плавающей арифметики» (для процессоров IBM PC, начиная с Intel-80486 и старше, это условие всегда выполняется).

Тип данных называется порядковым, если он состоит из счетного количества значений, которые можно пронумеровать. Отсюда следует, что на этом множестве значений существуют понятия «следующий» и «предыдущий».

Описание переменных. Для всех переменных величин, используемых в программе, должны быть указаны их типы. Это делается в разделе переменных программы. Структура раздела переменных показана на рис. 10.
 

Пример раздела переменных программы:

Var          m,n,k: Integer;

х,у,z: Real;

Symbol: Char;

Константы. Тип константы определяется по контексту, т.е. по форме ее записи в программе.

Целые десятичные константы записываются в обычной форме целого числа со знаком или без знака, например 25, -24712, 376.

Целые шестнадцатеричные константы записываются с префиксом $. Они должны находиться в диапазоне от $00000000 до $FFFFFFFF.

Вещественные константы с фиксированной точкой записываются в обычной форме десятичного числа с дробной частью. Разделитель целой и дробной части — точка, например: 56.346, 0.000055, -345678.0.

Вещественные константы с плавающей точкой имеют форму:

<мантисса>Е<порядок>

Здесь мантисса — целое или вещественное число с фиксированной точкой, порядок — целое число со знаком или без, например 7Е-2 (7∙10-2), 12.25Е6 (12,25∙106), 1Е-25 (10-25).

Символьная константа — любой символ алфавита, заключенный в апострофы, например, 'W, '!', '9'.

Логическая константа — одно из двух слов: true, false.

Строковая константа — строка символов, заключенная в апострофы, например Turbo Pascal', 'Ответ:', '35-45-79'. Максимальная длина — 255 символов.

Константе может быть поставлено в соответствие определенное имя. Назначение имени константе производится в разделе констант программы. Структура раздела констант показана на рис. 11.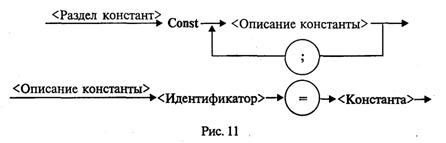
 

Пример: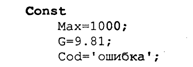
 

В дополнение к сказанному заметим, что в Турбо Паскале допустимо употребление типизированных констант. Типизированная константа аналогична переменной, которой задается начальное значение. Причем происходит это на этапе компиляции. Описание типизированной константы приведено на рис. 12.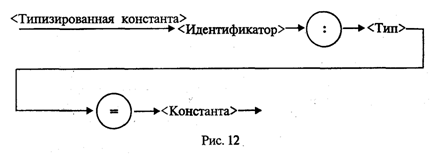
 

Пример:
 

В Турбо Паскале имеется ряд имен, зарезервированных за определенными значениями констант. Ими можно пользоваться без предварительного определения в программе (табл. 3.2).

Таблица 3.2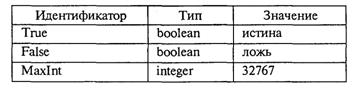
 

Типы пользователя. Один из принципиальных моментов состоит в том, что пользователю разрешается определять свои типы данных. Типы пользователя всегда базируются на стандартных типах данных Паскаля.

Для описания типов пользователя в Паскале существует раздел типов, структура которого представлена на рис. 13.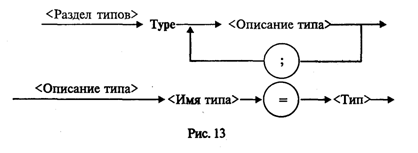
 

Перечисляемый тип (рис. 14) задается непосредственно перечислением всех значений, которые может принимать переменная данного типа.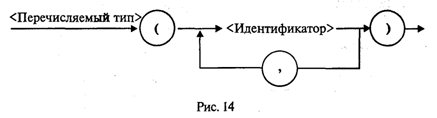
 

Определенное имя типа затем используется для описания переменных. Например: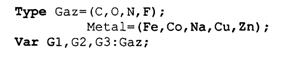
 

Здесь Gaz и Metal — имена перечисляемых типов, которые ставятся в соответствие переменным Gl, G2, G3 и Metl, Met2. Переменной Day назначается перечисляемый тип, которому не присвоено имя.

Значения, входящие в перечисляемый тип, являются константами. Действия над ними подчиняются правилам, применимым к константам. Каждое значение в перечисляемом типе занимает в памяти 2 байта. Поэтому число элементов не должно превышать 65535.

Перечисляемый тип — упорядоченное множество. Его элементы пронумерованы начиная от 0 в порядке следования в описании.

В программе, в которой присутствует данное выше описание, возможен такой фрагмент:
 

Интервальный тип (рис. 15) задается как упорядоченное ограниченное подмножество некоторого порядкового типа.

Порядковый номер первой константы не должен превышать номера второй константы в соответствующем базовом типе.

При исполнении программы автоматически контролируется принадлежность значений переменной интервального типа установленному диапазону. При выходе из диапазона исполнение программы прерывается.

Пример:

Арифметические операции, функции, выражения.Арифметический оператор присваивания

К арифметическим типам данных относятся группы вещественных и целых типов. К ним применимы арифметические операции и операции отношений.

Операции над данными бывают унарными (применимые к одному операнду) и бинарными (применимые к двум операндам). Унарная арифметическая операция одна. Это операция изменения знака. Ее формат:
 

Бинарные арифметические операции стандартного Паскаля описаны в табл. 3.3. В ней I обозначает целые типы, R — вещественные типы.

Таблица 3.3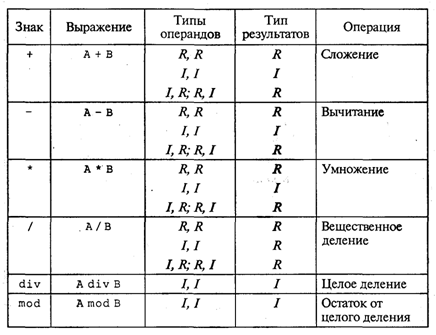
 

К арифметическим величинам могут быть применены стандартные функции Паскаля. Структура обращения к функции представлена на рис. 16.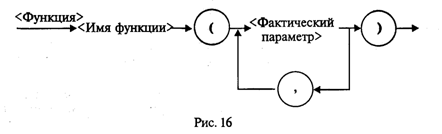

Функция выступает как операнд в выражении. Например, в следующем операторе присваивания

операндами являются три функции: sin, ln, cos. Их запись такая же, как в математике. Аргументы называются фактическими параметрами и являются в общем случае выражениями арифметического типа. Аргументы записываются в круглых скобках. Результат вычисления функции — величина соответствующего типа.

Табл. 3.4 содержит описания математических стандартных функций Турбо Паскаля.

Таблица 3.4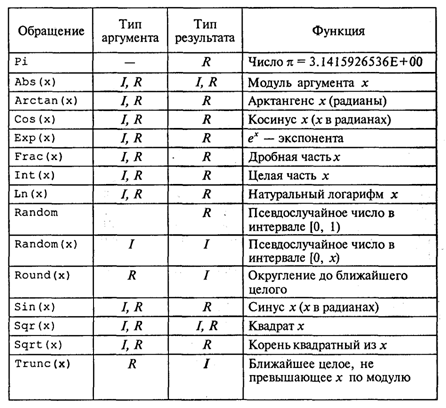
 

Арифметическое выражение задает порядок выполнения действий над числовыми величинами. Арифметические выражения содержат арифметические операции, функции, операнды, круглые скобки. Одна константа или одна переменная — простейшая форма арифметического выражения.

Например, запишем по правилам Паскаля следующее математическое выражение:
 

На Паскале это выглядит так:
 

Для того чтобы правильно записывать арифметические выражения, нужно соблюдать следующие правила:

1. Все символы пишутся в строчку на одном уровне. Проставляются все знаки операций (нельзя пропускать знак умножения).

2. Не допускаются два следующих подряд знака операций (нельзя A+-B; можно А+(-B)).

3. Операции с более высоким приоритетом выполняются раньше операций с меньшим приоритетом. Порядок убывания приоритетов:

• вычисление функции;

• унарная операция смены знака (-);

• *, /, div, mod;

• +, -.

4. Несколько записанных подряд операций одинакового приоритета выполняются последовательно слева направо.

5. Часть выражения, заключенная в скобки, вычисляется в первую очередь. (Например, (A+B) * (C—D) — умножение производится после сложения и вычитания.)

Не следует записывать выражений, не имеющих математического смысла. Например, деление на нуль, логарифм отрицательного числа и т. п.

Пример. Цифрами сверху указан порядок выполнения операций:

Данное арифметическое выражение соответствует следующей математической формуле: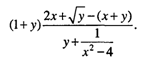

В Паскале нет операции или стандартной функции возведения числа в произвольную степень. Для вычисления xy рекомендуется поступать следующим образом:

• если у — целое значение, то степень вычисляется через умножение; например, х3 → х ∙ х ∙ х; большие степени следует вычислять умножением в цикле;

• если у — вещественное значение, то используется следующая математическая формула: хy = eyln(x).

На Паскале это будет выглядеть так:

Очевидно, что при вещественном у не допускается нулевое или отрицательное значение х. Для целого у такого ограничения нет.

Например,

На Паскале это будет так:
 

Выражение имеет целый тип, если в результате его вычисления получается величина целого типа. Выражение имеет вещественный тип, если результатом его вычисления является вещественная величина.

Арифметический оператор присваивания имеет структуру, представленную на рис. 17.
 

Например:
 

Порядок выполнения оператора присваивания нами уже рассматривался. Следует обратить особое внимание на следующее правило: типы переменной и выражения должны быть одинаковыми. Исключение составляет случай, когда выражение имеет целый тип, а переменная — вещественный.

Упражнения

1. Для следующих формул записать соответствующие арифметические выражения на Паскале: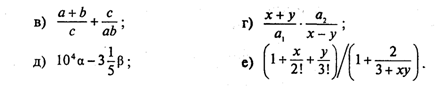
 

2. Записать математические формулы, соответствующие следующим выражениям на Паскале: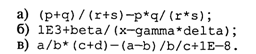
 

3. Почему в Паскале аргумент функции всегда записывают в скобках (например, пишут ln(5), а не ln5)?

4. Для следующих формул записать соответствующие арифметические выражения на Паскале: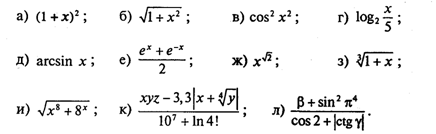
 

5. Вычислить значения выражений:
 

6. Определить тип выражения:
 

7. Если у — вещественная переменная, а п — целая, то какие из следующих операторов присваивания правильные, а какие нет: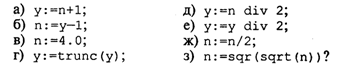
 

8. Поменять местами значения целых переменных х и у, не используя дополнительные переменные. Найдя такой алгоритм, определить, в чем его недостаток по сравнению с методом обмена через третью переменную. Можно ли его применять для вещественных чисел?

9. Присвоить целой переменной h значение цифры, стоящей в разряде сотен в записи положительного целого числа k (например, если k = 28796, то h = 7).

10. Целой переменной S присвоить значение суммы цифр трехзначного целого числа k.

11. Какую задачу решает следующая программа?
 

Можно ли того же самого результата достичь более простым способом?

Ввод с клавиатуры и вывод на экран

Ввод данных — это передача информации от внешних устройств в оперативную память. Вводятся, как правило, исходные данные решаемой задачи. Вывод — обратный процесс, когда данные передаются из оперативной памяти на внешние носители (принтер, дисплей, магнитные устройства и т.д.). Результаты решения всякой задачи должны быть выведены на один из этих носителей.

Основными устройствами ввода-вывода у персонального компьютера являются клавиатура и дисплей (экран монитора). Именно через эти устройства главным образом осуществляется диалог между человеком и ПК.

Процедура ввода с клавиатуры имеет следующий формат:

Read(<cписок ввода>)

где <список ввода> — это последовательность имен переменных, разделенных запятыми. Слово read переводится как читать. (Точнее говоря, Read — это оператор обращения к стандартной процедуре ввода.)

Например,
 

При выполнении этого оператора происходит прерывание работы компьютера, после чего пользователь должен набрать на клавиатуре значения переменных а, b, с, d, отделяя их друг от друга пробелами. При этом вводимые значения высвечиваются на экране. В конце нажимают клавишу Enter. Значения должны вводиться в строгом соответствии с синтаксисом Паскаля.

Пример:
 

Набираем на клавиатуре:
 

Если в программе имеется несколько операторов Read, то данные для них вводятся потоком, т. е. после считывания значений переменных для одного оператора Read данные для следующего оператора читаются из той же строки на экране, что и для предыдущего до окончания строки, затем происходит переход на следующую строку.

Пример:
 

Набираем на клавиатуре:
 

Другой вариант оператора ввода с клавиатуры имеет вид:
 

Здесь слово ReadLn означает read line — читать строку. Этот оператор отличается от Read только тем, что после считывания последнего в списке значения для одного оператора ReadLn данные для следующего оператора будут считываться с начала новой строки. Если в предыдущем примере заменить операторы Read на ReadLn:
 

то ввод значений будет происходить из двух строк:
 

Оператор вывода на экран (обращение к стандартной процедуре вывода) имеет следующий формат:
 

Здесь элементами списка вывода могут быть выражения различных типов (в частности, константы и переменные).

Пример:
 

При выводе на экран нескольких чисел в строку они не отделяются друг от друга пробелами

Программист сам должен позаботиться о таком разделении. Пусть, например, I = 1; J = 2, К = 3. Тогда, написав в программе

получим на экране строку: 1 2 3. После вывода последнего символа курсор остается в той же строке. Следующий вывод на экран будет начинаться с этой позиции курсора.

Второй вариант процедуры вывода на экран:

Слово WriteLn — write line — означает писать строку. Его действие отличается от оператора Write тем, что после вывода последнего в списке значения происходит перевод курсора к началу следующей строки. Оператор WriteLn, записанный без параметров, вызывает перевод строки.

Форматы вывода. В списке вывода могут присутствовать указатели форматов вывода (форматы). Формат определяет представление выводимого значения на экране. Он отделяется от соответствующего ему элемента двоеточием. Если указатель формата отсутствует, то машина выводит значение по определенному правилу, предусмотренному по умолчанию.

Ниже кратко, в справочной форме, приводятся правила и примеры бесформатного и форматированного вывода величин различных типов. Для представления списка вывода здесь будут использованы следующие обозначения:

I, Р, Q — целочисленные выражения;

R — выражение вещественного типа;

В — выражение булевского типа;

Ch — символьная величина;

S — строковое выражение;

# — цифра;

* — знак «+» или «—»;

_ — пробел.

Форматы процедуры Write

I — выводится десятичное представление величины I, начиная с позиции расположения курсора:
 

I:Р— выводится десятичное представление величины I в крайние правые позиции поля шириной Р:

R — в поле шириной 18 символов выводится десятичное представление величины R в формате с плавающей точкой. Если R ≥ 0,0, используется формат _#.##########Е*##. Если R < 0,0, то формат имеет вид _-#.##########Е*##:

R:Р — в крайние правые позиции поля шириной Р символов выводится десятичное представление значения R в нормализованном формате с плавающей точкой. Минимальная длина поля вывода для положительных чисел составляет 7 символов, для отрицательных — 8 символов. После точки выводится по крайней мере одна цифра:
 

R:P:Q — в крайние правые позиции поля шириной Р символов выводится десятичное представление значения R в формате с фиксированной точкой, причем после десятичной точки выводится Q цифр (0 ≤ Q ≤ 24), представляющих дробную часть числа. Если Q = 0, то ни дробная часть, ни десятичная точка не выводятся. Если Q > 24, то при выводе используется формат с плавающей точкой:

Управление символьным выводом на экран

Использование для вывода на экран только процедур Write и WriteLn дает программисту очень слабые возможности для управления расположением на экране выводимого текста. Печать текста может производиться только сверху вниз, слева направо. Невозможны возврат к предыдущим строкам, стирание напечатанного текста, изменение цвета символов и т.д.

Дополнительные возможности управления выводом на экран дают процедуры и функции модуля CRT.

Для установления связи пользовательской программы с модулем перед разделами описаний должна быть поставлена строка

Uses CRT

Для работы с модулем CRT необходимо познакомиться со следующими понятиями: режимы экрана, координаты на экране, текстовое окно, цвет фона и цвет символа.

Режимы экрана. Вывод на экран может происходить в текстовом или графическом виде (на графических дисплеях). Мы здесь будем говорить только о текстовом выводе.

Дисплеи бывают монохроматические (черно-белые) и цветные. Монохроматические дисплеи могут работать только в черно-белом режиме; цветные — как в черно-белом, так и в цветном. Кроме того, текстовые режимы различаются по количеству символьных строк и столбцов, умещающихся на экране.

В модуле CRT каждый режим имеет определенный номер, за которым закреплено символическое имя (описанная константа). Для установки режима экрана используется процедура

TextMode(<номер режима>)

При обращении к процедуре номер режима может задаваться как числом, так и именем соответствующей константы. Например, два оператора

TextMode(1);

TextMode(CO40);

эквивалентны.

Как правило, исходный режим экрана, устанавливаемый по умолчанию, — СO80 (на цветных дисплеях).

Координаты позиции. Каждая символьная позиция на текстовом экране определена двумя координатами (X, Y). Координата Х — позиция в строке. Для крайней левой позиции в строке Х = 1.. Координата Y — номер строки, в которой находится символ. Строки нумеруются сверху вниз.

Например, в режиме 80 х 25 символ в верхнем левом углу имеет координаты (1; 1); символ в нижнем правом углу — (80; 25); символ в середине экрана — (40; 13).

Для установления курсора на экране в позицию с координатами (X, Y) в модуле CRT существует процедура:

GoToXY(X,Y)

Здесь координаты курсора задаются выражениями типа Byte.

Вот пример программы, которая очищает экран и выставляет в центре экрана символ *:

Uses CRT;

Begin

CIrScr;

GoToXY(40,13);

Write('*')

End.

Используемая здесь процедура ClrScr производит очистку экрана.

Текстовое окно. Прямоугольное пространство на экране, в которое производится вывод символов, называется текстовым окном. Положение окна определяется координатами верхнего левого угла и нижнего правого угла прямоугольника. Если окно занимает весь экран, то в режиме 80 х 25 его координаты (1; 1) — (80; 25). Таким является исходное окно. Изменить положение и размер текстового окна можно с помощью процедуры

Window(Xl,Yl,X2,Y2)

Здесь аргументы — величины типа Byte; (X1, Yl) — координаты верхнего левого угла, (Х2, Y2) — координаты правого нижнего угла окна. После определения окна попытки вывода символов за его пределы оказываются безрезультатными. Повторное обращение к процедуре window с новыми параметрами отменяет предыдущее назначение.

Управление цветом. На современных цветных дисплеях типа EGA, VGA, SVGA в текстовом режиме экрана можно использовать 16 цветов.

В модуле CRT объявлены константы, имена которых представляют собой английские названия цветов, а соответствующие им значения — порядковые номера этих цветов.

Процедура назначения цвета фона:

TextBackGround(Color)

Здесь аргумент — величина типа Byte, задающая номер цвета.

Процедура назначения цвета символа:

TextColor(Color)

Если цвет фона назначается до очистки текстового окна, то после очистки окно заливается этим цветом. Если фон устанавливается после очистки экрана, то чистое окно будет иметь черный цвет (по умолчанию), а назначенный цвет фона будет устанавливаться в тех позициях, в которые выводятся символы.

Вот пример программы, в которой по очереди откроются четыре окна, и каждое из них будет залито своим фоновым цветом:

Uses CRT;

Begin

Window(1,1,40,12);

TextBackGround(White); CIrScr;

Window(41,1,80,12);

TextBackGround(Red); CIrScr;

Window(l,13,40,25);

TextBackGround(LightRed); CIrScr;

Window(41,13,80,25);

TextBackGround(Green); CirScr;

End.

По следующей программе на белом фоне в середине экрана будут выведены номера первых пятнадцати цветов. Каждый номер будет того цвета, который он обозначает.

Uses CRT;

Var I: Byte;

Begin

TextBackGround(White) ;

CIrScr;

GoToXY(l,12);

For I:=0 To 14 Do

Begin

TextColor(I);

Write(1:5) ;

End

End.

Кратко опишем еще несколько процедур управления текстовым экраном из модуля CRT. Все эти процедуры не имеют параметров.

Процедура ClrEOL. Стирает часть строки от текущей позиции курсора до конца этой строки в окне. При этом положение курсора не меняется.

Процедура DelLine. Уничтожает всю строку с курсором. Нижние строки сдвигаются на одну вверх.

Процедура InsLine. Вставляет пустую строку перед строкой, в которой стоит курсор.

Процедуры LowVideо, NormVideo, HighVideо. Устанавливают режимы пониженной, нормальной и повышенной яркости символов соответственно.

Весьма полезной является функция KeyPressed из модуля CRT. При исполнении этой функции происходит опрос клавиатуры и определяется, не нажата ли какая-нибудь клавиша. В результате функция выдает логическое значение True, если нажата любая клавиша, и значение False в противном случае. Часто эту функцию используют для организации задержки окна результатов на экране (после выполнения программы Турбо Паскаль вызывает на экран окно редактора). Перед концом программы записывается следующий оператор:

Repeat Until KeyPressed;

Это пустой цикл, который «крутится на месте» до нажатия какой-либо клавиши. В это время на экране окно результатов. После нажатия на клавишу значение KeyPressed станет равно True, цикл завершится, будет выполнен переход на метку End и на экран вернется окно редактора. Этот прием можно использовать для задержки выполнения программы в любом ее месте.

В приведенную выше программу получения на экране четырех разноцветных окон внесем следующее дополнение: после установки четырехцветного экрана выполнение программы останавливается и изображение сохраняется; затем после нажатия на любую клавишу экранвозвращается в исходный режим (80 х 25, черный фон, белые символы). Для этого перед концом программы нужно добавить следующее:

Repeat Until KeyPressed;

Window(1,1,80,25);

TextBackGround(Black);

CIrScr;

О других процедурах и функциях модуля CRT читайте в книгах по Турбо Паскалю.

Упражнения

1. Что будет напечатано в результате работы программы

Program Roots;

Var B,C,D: Real;

Begin

Read(B,C);

D:=Sqrt(Sqr(B)-4*C);

WriteLn('xl=',(-B+D)/2,

   'x2=',(-B-D)/2)

End.

если в качестве исходных данных заданы числа 10 и —20?

2. Что будет напечатано в результате работы программы

Program Less;

Var X:Real; T:Boolean;

Begin

Read(X);

T:=X<Round(X);

Read(X); 

T:=T And (X<Trunc(X)) ;

WriteLn(T)

End.

если последовательно вводятся два значения: 34, 79?

3. Что будет напечатано в результате работы программы

Program ABC;

Var A,B: Integer;

Begin

Read(A,B,A);

WriteLn(A,B:2,A:5)

End.

если последовательно вводятся три числа: 36, —6, 2345?

4. Составьте программу вычисления суммы двух целых чисел, которая будет вести диалог с пользователем в следующем виде (на месте многоточий — вводимые и выводимые числа):

ВВЕДИТЕ ДВА СЛАГАЕМЫХ     

а=............

b=............

РЕЗУЛЬТАТ ВЫЧИСЛЕНИЙ:

а+b=.............

Логические величины, операции, выражения. Логический оператор присваивания

Прямое отношение к программированию имеет дисциплина, которая называется математической логикой. Основу математической логики составляет алгебра логики, или исчисление высказываний. Под высказыванием понимается любое утверждение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, «Луна — спутник Земли» — истинно; «5 > 3» — истинно; «Москва — столица Китая» — ложно; «1 = 0» — ложно. Истина или ложь являются логическими величинами. Логические значения приведенных выше высказываний однозначно определены; другими словами, их значения являются логическими константами.

Логическое значение неравенства х < 0, где х — переменная, является переменной величиной. В зависимости от значения х оно может быть либо истиной, либо ложью. В связи с этим возникает понятие логической переменной.

Основы формального аппарата математической логики создал в середине XIX в. английский математик Джордж Буль. В его честь исчисление высказываний называют булевой алгеброй, а логические величины — булевскими.

Одиночные высказывания могут быть объединены в составные логические формулы с помощью логических операций.

Имеются три основные логические операции: отрицание, конъюнкция (логическое умножение) и дизъюнкция (логическое сложение).

Операция отрицания обозначается в математической логике значком ¬ и читается как частица не. Это одноместная операция.

Например, ¬ (x = у) читается «не (х равно y)». В результате получится истина, если х не равно у, и ложь, если х равно у. Отрицание изменяет значение логической величины на противоположное.

Операция конъюнкции обозначается значком & и читается как частица и. Это двухместная операция. Например, (х > 0) & (х < 1) читается «х больше 0 и х меньше 1». Данная логическая формула примет значение истина, если х 

В Паскале логические значения обозначаются служебными словами false (ложь) и true (истина), а идентификатор логического типа — boolean.

Кроме величин (констант и переменных) типа boolean логические значения false, true принимают результаты операций отношения.

Операции отношения (рис. 18) осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними.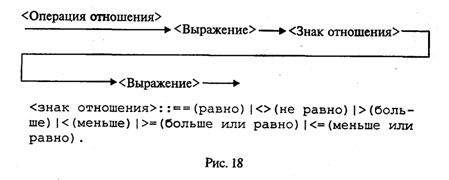
 

Примеры записи отношений: х<у; a+b>=c/d; abs(m-n)<=l. Примеры вычисления значений отношений:
 

Логические операции выполняются над операндами булева типа. Имеются четыре логические операции: Not — отрицание; And — логическое умножение (конъюнкция); Or — логическое сложение (дизъюнкция). Кроме этих трех обязательных операций в Турбо Паскале имеется еще операция — исключающее ИЛИ. Ее знак — служебное слово Хоr. Это двухместная операция, которая в результате дает значение истина, если оба операнда имеют разные логические значения.

Операции перечислены в порядке убывания приоритетов. Результаты логических операций для различных значений операндов приведены в табл. 3.5.

Таблица 3.5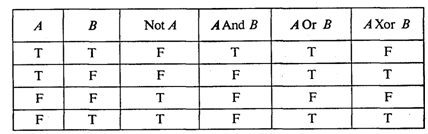
 

Операции отношения имеют самый низкий приоритет. Поэтому если операндами логической операции являются отношения, то их следует заключать в круглые скобки. Например, математическому неравенству 1 ≤ х ≤ 50 соответствует следующее логическое выражение:

(1<=X) And (X<=50)

Логическое выражение есть логическая формула, записанная на языке программирования. Логическое выражение состоит из логических операндов, связанных логическими операциями и круглыми скобками. Результатом вычисления логического выражения является булева величина (false или true). Логическими операндами могут быть логические константы, переменные, функции, операции отношения. Один отдельный логический операнд является простейшей формой логического выражения.

Примеры логических выражений (здесь d, b, с — логические переменные; х, у — вещественные переменные; k — целая переменная):
 

Если d=true; b=false; c=true; x=3.0; y=0.5; k=5, то результаты вычисления будут следующими:
 

В примере использована логическая функция odd(k). Это функция от целого аргумента k, которая принимает значение true, если значение k нечетное, и false, если k четное.

Логический оператор присваивания имеет структуру, представленную на рис. 19.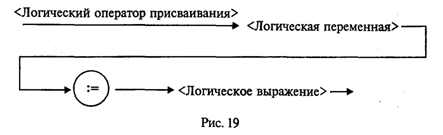
 

Примеры логических операторов присваивания:

1) d:=true;

2) b:=(x>y) and (k<>0);

3) c:=d or b and not (odd(k) and d).

Функции, связывающие различные типы данных

В табл. 3.6 приводится список стандартных функций, обеспечивающих связь между различными типами данных.

Таблица 3.6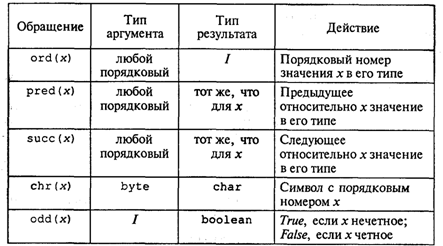
 

Функции ord, pred и succ применимы только к порядковым типам. Из простых типов это все, кроме вещественного.

Функция ord, применяемая к целому числу, дает его собственное значение. Например,

ord(-35)=-35; ord(128)=128

Если аргумент целый, то, например, оператор y:=pred(x) эквивалентен у:=х-1, а у:=succ(x) эквивалентен у:=х+1.

Для символьного типа аргумента эти функции дают соответственно предыдущий и следующий символ в таблице внутренней кодировки. Поскольку латинский алфавит всегда упорядочен по кодам, т.е.

ord('a')<ord('b')<…<-Ord('z'),

то, например,

pred('b')='a', a succ('b')='c'

То же относится и к цифровым литерам:

pred('5')='4'; succ('5')='6'

Функция chr (x) является обратной к функции ord(x), если х — символьная величина.

Это можно выразить формулой

chr(ord(x))=х,

где х — символьная величина.

Например, для кода ASCII справедливо

ord('a')=97; chr(97)='a'

В некоторых случаях возникает задача преобразования символьного представления числа в числовой тип. Например, нужно получить из литеры '5' целое число 5. Это делается так:

N:=ord('5')-ord('0'),

где N — целая переменная. Здесь использован тот факт, что код литеры '5' на пять единиц больше кода '0'.

Булевский тип также является порядковым. Порядок расположения двух его значений таков: false, true. Отсюда справедливы следующие отношения:

ord(false)=0, succ(false)=true,

ord(true)=1, pred(true)=false

Вот интересный пример. Пусть х, у, z — вещественные переменные. Как вы думаете, какую задачу решает следующий оператор:

z:=x*ord(x>=y)+y*ord(y>x)

Ответ такой: z = mах(х, у). Как видите, эту задачу можно решить, не используя условного оператора if...then...else.

Упражнения

1. Вычислить значения логических выражений:

а) К mod 7=K div 5-1 при К=15;

б) odd(trunc(10*P)) при Р=0.182;

В) not odd(n)при n=0;

г) t and (P mod 3=0) при t=true, P=10101;

Д) (x*y<>0) and (y>x) при х=2, y=l;

e) a or not b при a=false, b=true.

2. Если a=true и х=1, то какое значение получит логическая переменная d после выполнения оператора присваивания:

a) d:=x<2; б) d:=not a or odd(x); в) d:=ord(a)ox

3. Написать оператор присваивания, в результате выполнения

которого логическая переменная t получит значение true, если высказывание истинно, и значение false — в противном случае, для следующих высказываний:

а) из чисел х, у, z только два равны между собой;

б) х — положительное число;

в) каждое из чисел х, у, z положительно;

г) только одно из чисел х, у, z положительно;

д) р делится нацело на q;

e) цифра 5 входит в десятичную запись трехзначного целого числа k.

Логические выражения в управляющих операторах

Алгоритмическая структура ветвления программируется в Паскале с помощью условного оператора. Раньше мы его описывали в таком виде:

If <условие> Then <оператор 1> Else <оператор 2>;

Кроме того, возможно использование неполной формы условного оператора:

If <условие> Then <оператор>;

Теперь дадим строгое описание условного оператора в форме синтаксической диаграммы (рис. 20).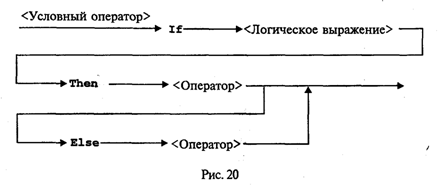
 

То, что мы раньше называли условием, есть логическое выражение, которое вычисляется в первую очередь. Если его значение равно true, то будет выполняться <оператор 1> (после Then), если false, то <оператор 2> (после Else) для полной формы или сразу следующий оператор после условного для неполной формы (без Else).

Пример 1. По длинам трех сторон треугольника а, b, с вычислить его площадь.

Для решения задачи используется формула Герона
 

где р = (а + b + с) / 2 — полупериметр треугольника. Исходные данные должны удовлетворять основному соотношению для сторон треугольника: длина каждой стороны должна быть меньше длин двух других сторон.

Имея возможность в одном условном операторе записывать достаточно сложные логические выражения, мы можем сразу «отфильтровать» все варианты неверных исходных данных.

Program Geron;

Var A,B,C,P,S: Real;

Begin

WriteLn('Введите длины сторон треугольника:');

Write('а='); ReadLn(A) ;

Write('b='); ReadLn(В);

Write ('c='); ReadLn(C);

If (A>0) And (B>0) And (00) And (A+B>C)

And (B+С>A) And (A+C>B)

Then Begin

P:=(A+B+C)/2;

S:=Sqrt(P*(P-A)*(P-B)*(P-C));

WriteLn('Площадь=',S)

End

Else WriteLn('Неверные исходные данные')

End.

Теперь рассмотрим синтаксическую диаграмму оператора цикл-пока, или цикл с предусловием (рис. 21).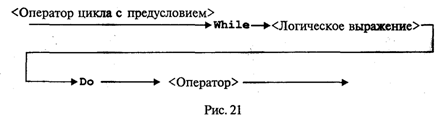
 

Сначала вычисляется <Логическое выражение>. Пока его значение равно true, выполняется <0ператор> — тело цикла. Здесь <Oператор> может быть как простым, так и составным.

Пример 2. В следующем фрагменте программы на Паскале вычисляется сумма конечного числа членов гармонического ряда
 

Суммирование прекращается, когда очередное слагаемое становится меньше ε или целая переменная i достигает значения MaxInt.

S:=0;

I:=l;

While (l/I>=Eps) And (I<MaxInt) Do

Begin

S:=S+1/I;

I:=1+1

End;

Синтаксическая диаграмма оператора цикл-до, или цикл с постусловием, представлена на рис. 22.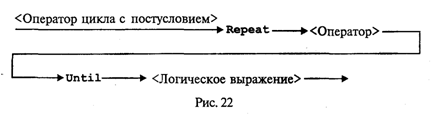

Исполнение цикла повторяется до того момента, когда <Логическое выражение> станет равным true.

Предыдущая задача с использованием цикла с постусловием решается так:

S:=0;

I:=1;

Repeat

S:=S+1/I; I:=I+1

Until (1/I<Eps) Or (I>=MaxInt)

Цикл по параметру

Рассмотрим следующую простую задачу: требуется вычислить сумму целых чисел от M до N путем прямого суммирования. Здесь М и N — целые числа. Задачу можно сформулировать так: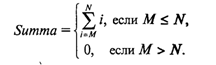
 

Алгоритм и программа решения этой задачи с использованием структуры цикл-пока представлены на рис. 23.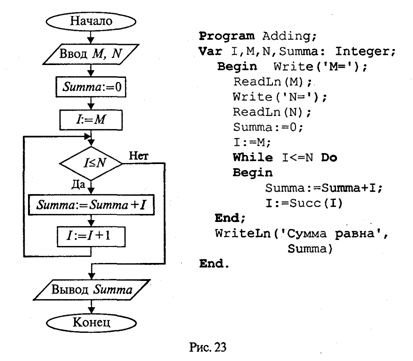
 

А теперь введем новый тип циклической структуры, который будет называться цикл по параметру, или цикл-для. Блок-схема и программа наПаскале для решения рассматриваемой задачи с использованием этой структуры приведены на рис. 24.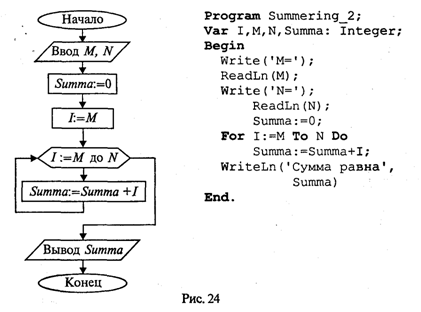
 

Здесь целая переменная I последовательно принимает значения в диапазоне от М до N. При каждом значении I выполняется тело цикла. После последнего выполнения цикла при I = N происходит выход из цикла на продолжение алгоритма. Цикл выполняется хотя бы один раз, если М ≤ N, и не выполняется ни разу при М > N.

В программе используется оператор цикла For, синтаксическая диаграмма которого представлена на рис. 25.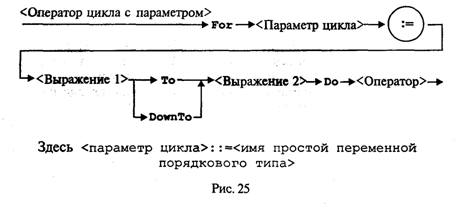
 

Выполнение оператора For в первом варианте (То) происходит по следующей схеме:

1. Вычисляются значения < Выражения 1> и < Выражения 2>. Это делается только один раз при входе в цикл.

2. Параметру цикла присваивается значение < Выражения 1>.

3. Значение параметра цикла сравнивается со значением < Выражения 2 >. Если параметр цикла меньше или равен этому значению, то выполняется тело цикла, в противном случае выполнение цикла заканчивается.

4. Значение параметра цикла изменяется на следующее значение в его типе (для целых чисел — увеличивается на единицу); происходит возврат к пункту 3.

Оператор цикла For объединяет в себе действия, которые при использовании цикла While выполняют различные операторы: присваивание параметру начального значения, сравнение с конечным значением, изменение на следующее.

Как известно, результат суммирования целых чисел не зависит от порядка суммирования. Например, в рассматриваемой задаче числа можно складывать и в обратном порядке, т.е. от N до М (N ≥ М). Для этого можно использовать второй вариант оператора цикла For:

Summa:=0 ;

For I:=N DownTo M Do

Summa:=Summa+I;

Слово DownTo буквально можно перевести как «вниз до». В таком случае параметр цикла изменяется по убыванию, т.е. при каждом повторении цикла параметр изменяет свое значение на предыдущее (равносильно i:=pred(i)). Тогда ясно, что цикл не выполняется ни разу, если N < М.

Работая с оператором For, учитывайте следующие правила:

• параметр цикла не может иметь тип Real;

• в теле цикла нельзя изменять переменную «параметр цикла»;

• при выходе из цикла значение переменной-параметра является неопределенным.

В следующем примере в качестве параметра цикла For используется символьная переменная. Пусть требуется получить на экране десятичные коды букв латинского алфавита. Как известно, латинские буквы в таблице кодировки упорядочены по алфавиту. Вот фрагмент такой программы:

For С:='а' То 'z' Do

Write (С,'-',Ord(C));

Здесь переменная С имеет тип Char.

А теперь подумайте сами, как вывести кодировку латинского алфавита в обратном порядке (от 'z' до 'а').

Упражнения

1. Составить программу полного решения квадратного уравнения (алгоритм см. в разд. 1.3).

2. Используя операторы цикла While, Repeat и For, составить три варианта программы вычисления N!.

3. Составить программу, по которой будет вводиться последовательность символов до тех пор, пока не встретится маленькая или большая латинская буква z. Подсчитать, сколько раз среди вводимых символов встречалась буква W.

4. Вычислить сумму квадратов всех целых чисел, попадающих в интервал (ln х, еx), х > 1.

5. Вычислить количество точек с целочисленными координатами, попадающих в круг радиуса R (R > 0) с центром в начале координат.

6. Напечатать таблицу значений функции sin x и cos x на отрезке [0, 1] с шагом 0,1 в следующем виде:
 

7. Напечатать в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр.

8. Дано целое п > 2. Напечатать все простые числа из диапазона [2, п].

Подпрограммы

С понятием вспомогательного алгоритма вы уже знакомы (см. разд. 1.4). В языках программирования вспомогательные алгоритмы называются подпрограммами. В Паскале различаются две разновидности подпрограмм: процедуры и функции. Рассмотрим этот вопрос на примере следующей задачи: даны два натуральных числа a и b. Требуется определить наибольший общий делитель трех величин: а + b, |а – b|, а • b. Запишем это так: НОД (a + b, |а – b|, а • b).

Идея решения состоит в следующем математическом факте: если х, у, z — три натуральных числа, то НОД(х, у, z) = НОД(НОД(х, у), z). Иначе говоря, нужно найти НОД двух величин, а затем НОД полученного значения и третьего числа (попробуйте это доказать).

Очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения наибольшего общего делителя двух чисел. Эта задача решается с помощью известного алгоритма Евклида (см. раздел 1.3). Запишем его в форме процедуры на алгоритмическом языке.

Процедура Евклид(цел M,N,K);

нач

пока M<>N

нц

если M>N

то M:=M-N

иначе N:=N-M

кв

кц;

K:=M

кон

Здесь M и N являются формальными параметрами процедуры. M и N параметры-аргументы, K — параметр-результат. Основной алгоритм, решающий исходную задачу, будет следующим:

алг задача;

цел а,b,с;

нач ввод(а,b);

Евклид(а+b,|a-b|,с);

Евклид(с,а*b,с);

вывод(с)

кон.

Процедуры в Паскале. Основное отличие процедур в Паскале от процедур в Алгоритмическом языке (АЯ) состоит в том, что процедуры в Паскале описываются в разделе описания подпрограмм, а в АЯ процедура является внешней по отношению к вызывающей программе. Теперь посмотрим, как решение поставленной задачи программируется на Турбо Паскале.

Program NOD1;

Var А,В,С: Integer;

Procedure Evklid(M,N: Integer; Var К: Integer);

Begin

While M<>N Do

If M>N

Then M:=M-N

Else N:=N-M;

K:=M

End;

Begin

Write('a=');

ReadLn(A) ;

Write('b=');

ReadLn(B);

Evklid(A+B,Abs(A-B),C);

Evklid(C,A*B,C);

WriteLn('НОД=',C)

End.

В данном примере обмен аргументами и результатами между основной программой и процедурой производится через параметры (формальные и фактические). Существует и другой механизм обмена — через глобальные переменные. Но об этом чуть позже. А сейчас рассмотрим синтаксическую диаграмму описания процедуры (рис. 27).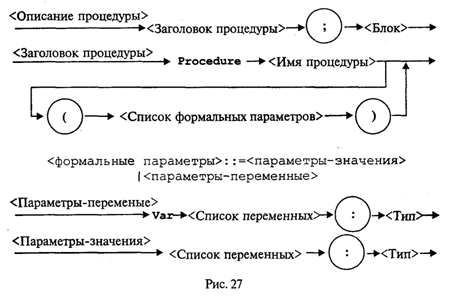
 

Из диаграммы видно, что процедура может иметь параметры, а может быть и без них

Чаще всего аргументы представляются как параметры-значения (хотя могут быть и параметрами-переменными). А для передачи результатов используются параметры-переменные.

Процедура в качестве результата может передавать в вызывающую программу множество значений (в частном случае — одно), а может и ни одного. Теперь рассмотрим правила обращения к процедуре. Обращение к процедуре производится в форме оператора процедуры (рис. 28).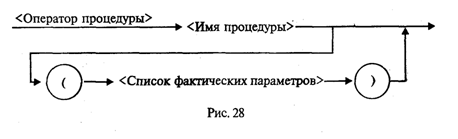
 

Если описана процедура с формальными параметрами, то и обращение к ней производится оператором процедуры с фактическими параметрами. Правила соответствия между формальными и фактическими параметрами: соответствие по количеству, соответствие по последовательности и соответствие по типам.

Первый вариант взаимодействия формальных и фактических параметров называется передачей по значению: вычисляется значение фактического параметра (выражения) и это значение присваивается соответствующему формальному параметру. Второй вариант взаимодействия называется передачей по имени: при выполнении процедуры имя формальной переменной заменяется на имя соответствующей фактической переменной (в откомпилированной программе имени переменной соответствует адрес ячейки памяти).

В рассмотренном нами примере формальные параметры М и N являются параметрами-значениями. Это аргументы процедуры. При обращении к ней первый раз им соответствуют значения выражений а + b и abs (а - b); второй раз — с и а • b. Параметр K является параметром-переменной. В ней получается результат работы процедуры. В обоих обращениях к процедуре соответствующим фактическим параметром является переменная с. Через эту переменную основная программа получает результат.

Теперь рассмотрим другой вариант программы, решающей ту же задачу. В ней используется процедура без параметров.

Program NOD2;

Var A,B,K,M,N: Integer;

Procedure Evklid;

Begin

While M<>N Do

If M>N

Then M:=M-N

Else N:=N-M;

K:=M

End;

Begin

Write('a=');

ReadLn(A);

Write('b=');

ReadLn(B);

M:=A+B;

N:=Abs(A-B);

Evklid;

M:=K;

N:=A*B;

Evklid;

WriteLn('HOД равен',K)

End.

Чтобы разобраться в этом примере, требуется объяснить новое для нас понятие: область действия описания.

Областью действия описания любого программного объекта (переменной, типа, константы и т.д.) является тот блок, в котором расположено это описание

Если данный блок вложен в другой (подпрограмма), то присутствующие в нем описания являются локальными. Они действуют только в пределах внутреннего блока. Описания же, стоящие во внешнем блоке, называются глобальными по отношению к внутреннему блоку. Если глобально описанный объект используется во внутреннем блоке, то на него распространяется внешнее (глобальное) описание.

В программе NOD1 переменные М, N, К — локальные внутри процедуры; переменные а, b, с — глобальные. Однако внутри процедуры переменные а, b, с не используются. Связь между внешним блоком и процедурой осуществляется через параметры.

В программе NOD2 все переменные являются глобальными. В процедуре Evklid нет ни одной локальной переменной (нет и параметров). Поэтому переменные М и N, используемые в процедуре, получают свои значения через оператор присваивания в основном блоке программы. Результат получается в глобальной переменной К, значение которой выводится на экран.

Использование механизма передачи через параметры делает процедуру более универсальной, независимой от основной программы. Однако в некоторых случаях оказывается удобнее использовать передачу через глобальные переменные. Чаще такое бывает с процедурами, работающими с большими объемами информации. В этой ситуации глобальное взаимодействие экономит память ЭВМ.

Функции. Теперь выясним, что такое подпрограмма-функция. Обычно функция используется в том случае, если результатом подпрограммы должна быть скалярная (простая) величина. Тип результата называется типом функции. В Турбо Паскале допускаются функции строкового типа. Синтаксическая диаграмма описания функции представлена на рис. 29.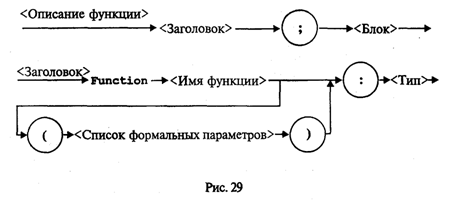

Как и у процедуры, у функции в списке формальных параметров могут присутствовать параметры-переменные и параметры-значения. Все это аргументы функции. Параметры вообще могут отсутствовать (если аргументы передаются глобально).

Программа решения рассмотренной выше задачи с использованием функции будет выглядеть следующим образом:

Program NOD3;

Var А,В,Rez:Integer;

Function Evklid(M,N:Integer):Integer;

Begin

While M<>N Do

If M>N

Then M:=M-N

Else N:=N-M;

Evklid:=M

End;

Begin

Write('a=');

ReadLn(A);

Write('b=');

ReadLn(B);

Rez:=Evklid(Evklid(A+B,Abs(A-B)),A*B);

WriteLn('NOD равен',Rez)

End.

Из примера

видно, что тело функции отличается от тела процедуры только тем, что в функции результат присваивается переменной с тем же именем, что и функция.

Обращение к функции является операндом в выражении. Оно записывается в следующей форме:

<Имя функции> (<Список фактических параметров>)

Правила соответствия между формальными и фактическими параметрами все те же. Сравнивая приведенные выше программы, можно сделать вывод, что программа NOD3 имеет определенные преимущества перед другими. Функция позволяет получить результат путем выполнения одного оператора присваивания. Здесь иллюстрируется возможность того, что фактическим аргументом при обращении к функции может быть эта же функция.

По правилам стандарта Паскаля возврат в вызывающую программу из подпрограммы происходит, когда выполнение подпрограммы доходит до ее конца (последний End). Однако в Турбо Паскале есть средство, позволяющее выйти из подпрограммы в любом ее месте. Это оператор-процедура Exit. Например, функцию определения наибольшего из двух данных вещественных чисел можно описать так:

Function Max(X,Y: Real): Real;

Begin

Max:=X;

If X>Y Then Exit Else Max:=Y

End;

Еще раз об области действия описаний. В Паскале неукоснительно действует следующее правило: любой программный объект (константа, переменная, тип и т.п.) должен быть описан перед использованием в программе. Иначе говоря, описание объекта должно предшествовать его первому появлению в других фрагментах программы. Это правило относится и к подпрограммам.

На рис. 30 схематически показана структура взаимного расположения описаний подпрограмм в некоторой условной программе. Попробуем, используя эту схему, разобраться в вопросе об области действия описаний подпрограмм.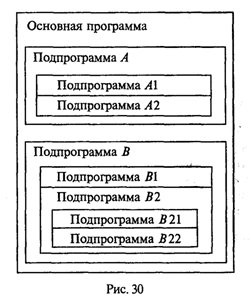

Любая подпрограмма может использоваться лишь в пределах области действия ее описания. Например, область действия подпрограмм А и В — основная программа. Поэтому из основной программы можно обратиться к подпрограммам А и В. В свою очередь, в подпрограмме В могут быть обращения к подпрограмме А; а из А нельзя обратиться к В, поскольку описание А предшествует описанию В. Подпрограммы А1 и А2 локализованы в подпрограмме A и могут использоваться только в ней; из А2 можно обратиться к A1, но не наоборот.

Из подпрограммы B1 можно обратиться к А, поскольку ее описание является глобальным по отношению к B1, но нельзя обратиться к А1, поскольку область действия описания А1 не распространяется на блок подпрограммы В.

Из подпрограммы В22 можнообратиться только к B21, B1, А. Объясните сами почему.

Все понятно? Если нет, то прочитайте еще раз этот раздел. Очень важно в нем разобраться.

Если одно и то же имя описано во внешнем блоке (глобально) и во внутреннем блоке (локально), то последнее описание (локальное) перекрывает первое в пределах внутреннего блока. Рассмотрим следующий пример:

Program Example1;               Program Example2;

Var X: Integer;                 Var X: Integer;

Procedure P;                    Procedure P;

Var X: Integer;                 Begin

Begin WriteLn('x=',X)               WriteLn('x=',X)

End;                            End;

Begin X:=1;                     Begin X:=l;

P                                     P

End.                            End.

Что выведется на экран в результате работы программы Example1 и Example2? Первая программа выдаст результат:

х=...

На месте многоточия будет какое-то произвольное значение, соответствующее неопределенной величине х. Вторая программа в результате даст

х=1

В первом случае переменная с именем х описана как глобально, так и локально. Но процедура выводит значение локальной переменной, которой ничего не присвоено. В этом примере идентификатором х обозначены две совершенно разные величины, им соответствуют две разные ячейки памяти.

Во втором примере переменная х одна на всю программу. Она описана глобально. Поэтому значение 1, присвоенное ей в основной программе, передается и в подпрограмму.

Далее разговор пойдет о ситуации на первый взгляд совершенно парадоксальной. Оказывается, подпрограмма в своем описании может содержать обращение к самой себе. Такая подпрограмма называется рекурсивной.

Рекурсивные подпрограммы. В математике рекурсивным называется определение любого понятия через самое себя. Классическим примером является определение факториала целого числа, большего или равного нулю: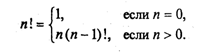
 

Здесь функция факториала определена через факториал. Нетрудно понять справедливость такого определения. Для п > 0
 

Вариант 0!=1 является тривиальным. Но это «опорное» значение, от которого начинается раскручивание всех последующих значений факториала:
 

Рассмотрим подпрограмму-функцию, использующую в своем описании приведенную выше рекурсивную формулу.

Function Factor(N: Pozint): Pozint;

Begin

If N=0

Then Factor:=1

Else Factor:=N*Factor(N-l)

End;

Предполагается, что тип PozInt объявлен глобально следующим образом:

Type PozInt=0..MaxInt;

Пусть в основной программе для вычисления в целой переменной х значения 3! используется оператор

X:=Factor(3);

При вычислении функции с аргументом 3 произойдет повторное обращение к функции Factor(2). Это обращение потребует вычисления Factor(1). И наконец, при вычислении Factor(0) будет получен числовой результат 1. Затем цепочка вычислений раскрутится в обратном порядке:

Factor(1)=l*Factor(0)=1

Factor(2)=2*Factor(1)=2

Factor(3)=3*Factor(2)=6.

Последовательность рекурсивных обращений к функции должна обязательно выходить на определенное значение. А весь маршрут последовательных вхождений машина запоминает в специальной области памяти, называемой стеком. Таким образом, выполнение рекурсивной функции происходит в два этапа: прямой ход — заполнение стека; обратный ход — цепочка вычислений по обратному маршруту, сохраненному в стеке.

Использование рекурсивных функций — красивый прием с точки зрения программистской эстетики. Однако этот путь не всегда самый рациональный. Рассмотренную задачу с п! можно решить так:

F:=l;

For I:=l To N Do

F:=F*I;

Очевидно, что такой вариант программы будет работать быстрее, чем рекурсивный. И в том случае, когда важнейшим является сокращение времени выполнения программы, следует отдать предпочтение последнему варианту.

В каждой конкретной реализации Паскаля имеется ограничение на количество рекурсивных обращений к подпрограмме (глубина рекурсии). Это связано с ограничением на размер стека. По этой причине можно попасть в ситуацию, когда рекурсивной подпрограммой вообще не удастся воспользоваться.

Рекурсивно определена может быть не только функция, но и процедура. Примеры использования рекурсивно-определенных процедур рассматриваются в пятой главе.

Упражнения

1. Составить программу вычисления площади кольца по значениям внутреннего и внешнего радиусов, используя подпрограмму вычисления площади круга (2 варианта: с процедурой и с функцией).

2. По координатам вершин треугольника вычислить его периметр, используя подпрограмму вычисления длины отрезка, соединяющего две точки.

3. Даны три целых числа. Определить, сумма цифр которого из них больше. Подсчет суммы цифр организовать через подпрограмму.

4. Определить площадь выпуклого четырехугольника по заданным координатам вершин. Использовать подпрограмму-функцию вычисления длины отрезка и подпрограмму-процедуру вычисления площади треугольника по формуле Герона.

5. Описать рекурсивную функцию pow(x, n) от вещественного х (х ≠ 0) и целого п, которая вычисляет величину хn по формуле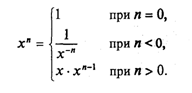
 

6. Даны натуральные числа п и т; найти НОД (n, т). Использовать программу, включающую в себя рекурсивную процедуру вычисления НОД, и основанную на соотношении НОД (n, т) = НОД (т, r), где r — остаток от деления п на т.

Вычисление рекуррентных последовательностей

Рекуррентная последовательность. Из курса математики известно понятие рекуррентной последовательности. Это понятие вводится так: пусть известно k чисел a1, ..., аk. Эти числа являются первыми числами числовой последовательности. Следующие элементы данной последовательности вычисляются так:
 

Здесь F— функция от k аргументов. Формула вида
 

называется рекуррентной формулой. Величина k называется глубиной рекурсии.

Другими словами, можно сказать, что рекуррентная последовательность — это бесконечный ряд чисел, каждое из которых, за исключением k начальных, выражается через предыдущие.

Примерами рекуррентных последовательностей являются арифметическая (1) и геометрическая (2) прогрессии:
 

Рекуррентная формула для указанной арифметической прогрессии:
 

Рекуррентная формула для данной геометрической прогрессии:
 

Глубина рекурсии в обоих случаях равна единице (такую зависимость еще называют одношаговой рекурсией). В целом рекуррентная последовательность описывается совокупностью начальных значений и рекуррентной формулы. Все это можно объединить в одну ветвящуюся формулу. Для арифметической прогрессии: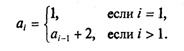
 

Для геометрической прогрессии: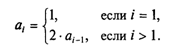
 

Следующая числовая последовательность известна в математике под названием чисел Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Начиная с третьего элемента каждое число равно сумме значений двух предыдущих, т. е. это рекуррентная последовательность с глубиной равной 2 (двухшаговая рекурсия). Опишем ее в ветвящейся форме: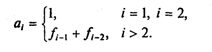
 

Введение представления о рекуррентных последовательностях позволяет по-новому взглянуть на некоторые уже известные нам задачи. Например, факториал целого числа п! можно рассматривать как значение n-го элемента следующего ряда чисел:
 

Рекуррентное описание такой последовательности выглядит следующим образом: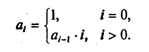
 

Программирование вычислений рекуррентных последовательностей. С рекуррентными последовательностями связаны задачи такого рода:

1) вычислить заданный (n-й) элемент последовательности;

2) математически обработать определенную часть последовательности (например, вычислить сумму или произведение первых n членов);

3) подсчитать количество элементов на заданном отрезке последовательности, удовлетворяющих определенным свойствам;

4) определить номер первого элемента, удовлетворяющего определенному условию;

5) вычислить и сохранить в памяти заданное количество элементов последовательности.

Данный перечень задач не претендует на полноту, но наиболее часто встречающиеся типы он охватывает. В четырех первых задачах не требуется одновременно хранить в памяти множество элементов числового ряда. В таком случае его элементы могут получаться последовательно в одной переменной, сменяя друг друга.

Пример 1. Вычислить п-й элемент арифметической прогрессии (1).

Var M,I: 0..Maxint;

A: Real;

Begin

Write('N=');

ReadLn(N);

A:=l;

For I: =2 To N Do

A:=A+2;

WriteLn('A(',N:l,')=',A:6:0)

End.

Рекуррентная формула ai = ai-­1 + 2 перешла в оператор А := А + 2.

Пример 2. Просуммировать первые п элементов геометрической прогрессии (2) (не пользуясь формулой для суммы первых n членов прогрессии).

Var N,1: 0..Maxint;

A,S: Real;

Begin

Write('N='); ReadLn(N);

A:=l;

S:=A;

For I: =2 To N Do

Begin

A:=2*A;

S:=S+A

End;

WriteLn('Сумма равна',S:6:0)

End.

При вычислении рекуррентной последовательности с глубиной 2 уже нельзя обойтись одной переменной. Это видно из следующего примера.

Пример 3. Вывести на печать первые п (п ≥ 3) чисел Фибоначчи. Подсчитать, сколько среди них четных чисел.

Var N,I,K,F,F1,F2: 0..Maxint;

Begin

Fl:=l; F2:=l;

K:=0;

WriteLn('F(l)=',Fl,'F(2)=',F2);

For I:=3 To N Do

Begin

F:=F1+F2;

WriteLn('F(',I:l,')=',F);

If Not Odd(F) Then K:=K+1;

F1:=F2; F2:=F

End;

WriteLn('Количество четных чисел в последовательности равно',К)

End.

Понадобились три переменные для последовательного вычисления двухшаговой рекурсии, поскольку для нахождения очередного элемента необходимо помнить значения двух предыдущих.

Пример 4. Для заданного вещественного х и малой величины ε (например, ε = 0,000001) вычислить сумму ряда

включив в нее только слагаемые, превышающие ε. Известно, что сумма такого бесконечного ряда имеет конечное значение, равное еx, где е = 2,71828... — основание натурального логарифма. Поскольку элементы этого ряда представляют собой убывающую последовательность чисел, стремящуюся к нулю, то суммирование нужно производить до первого слагаемого, по абсолютной величине не превышающего ε.

Если слагаемые в этом выражении обозначить следующим образом:

Пример 5. Для заданного натурального N и вещественного х (х > 0) вычислить значение выражения:
 

В этом случае рекуррентность не столь очевидна. Попробуем найти ее методом индукции. Будем считать, что искомое выражение есть N-й элемент последовательности следующего вида:
 

Отсюда видна связь:
 

Теперь поставленная задача решается очень просто:

Var A,X: Real; I,N: Integer;

Begin

Write('X='); ReadLn(X);

Write('N='); ReadLn(N);

A:= Sqrt(X);

For I:=2 To N Do

A:=Sqrt(X+A);

WriteLn('Ответ:',А)

End.

К решению всех перечисленных выше задач можно подойти иначе.

Вспомним о рекурсивно определенных подпрограммах. Посмотрите на описание арифметической прогрессии в форме рекуррентной последовательности. Из него непосредственно вытекает способ определения функции для вычисления заданного элемента прогрессии.

Сделаем это для общего случая, определив арифметическую прогрессию с первым членом а0 и разностью d: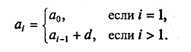
 

Соответствующая подпрограмма-функция выглядит так:

Function Progres(АО,D: Real;I: Integer): Real;

Begin

If I=1

Then Progres:=AO

Else Progres:=Progres(A0,D,I-1)+D

End;

Следующая программа выводит на экран первые 20 чисел Фибоначчи, значения которых вычисляет рекурсивная функция Fibon.

Var К: Byte;

Function Fibon(N: Integer): Integer;

Begin

If (N=1) Or (N=2)

Then Fibon:=1

Else Fibon:=Fibon(N-1)+Fibon(N-2)

End;

Begin

For K:=l To 20 Do WriteLn(Fibon(K))

End.

Горизонтальная ось X направлена слева направо, вертикальная ось Y — сверху вниз. На рисунке указаны предельные графические координаты, соответствующие режиму VGAHi.

Можно определить максимальные координаты по осям, соответствующие данному драйверу. Это делается с помощью двух целочисленных функций:

Function GetMaxX;
Function GetMaxY;
Графическое окно. Область вывода изображения может быть ограничена любым прямоугольником в пределах экрана. Такая область называется графическим окном. Существует процедура, устанавливающая положение графического окна на экране.
Заголовок процедуры назначения графического окна:
Procedure SetViewPort(X1,Y1,X2,Y2: Integer; Clip: Boolean);

Здесь (X1, Y1) — координаты левого верхнего угла окна; (Х2, Y2) — координаты правого нижнего угла окна; Clip — ограничитель фигур; если Clip=True, то все построения производятся только в пределах окна, в противном случае они могут выходить за его пределы.
После установки окна координаты точек внутри него отсчитываются от верхнего левого угла.
Существует понятие графического курсора (по аналогии с символьным курсором). Но в отличие от символьного курсора графический курсор на экране не виден. Графический курсор указывает на текущую позицию на экране. При входе в графический режим координаты текущей позиции равны (0, 0).

Процедура назначения координат графического курсора:

Procedure MoveTo(X,Y: Integer);
Здесь X, Y — устанавливаемые координаты курсора. Координаты указываются относительно левого верхнего угла окна или, если окно не установлено, экрана.

Процедура поставить точку — основная процедура получения изображения, поскольку любой рисунок складывается из точек. Состояние светящейся точки определяется координатами точки на экране и цветом точки.

Заголовок процедуры выставления точки на графическом экране:


Procedure PutPixel(X,Y: Integer; Color: Word);


Здесь X, Y — координаты точки, Color — цвет точки.

Пример 1. Следующая программа устанавливает по центру экрана графическое окно размером 100х100, заливает его желтым фоном и заполняет синими точками, расположенными через 4 позиции.


Uses Graph;
Var Driver,Mode: Integer;
X,Y,Xl,Yl,X2,Y2,Xc,Yc: Integer;
Begin
{Инициализация графического режима}
Driver:=Detect;
InitGraph(Driver, Mode,'C:\TP\BGI');

{Определение координат центра экрана}
Хс:=GetMaxX Div 2;
Yc:=GetMaxY Div 2;
{Определение координат графического окна}

X1:=Хс-50
Yl:=Yc-50
Х2:=Хс+50
Y2:=Yc+50
{Установка графического окна}
SetViewPort(Xl,Yl,X2,Y2,True);

{Установка цвета фона и очистка экрана}
SetBkColor(Yellow);
ClearDevice;
{Расстановка точек в окне)

For X:=l То 25 Do

For Y:=l To 25 Do

PutPixel(4*X,4*Y,Blue);

{Задержка изображения на экране до нажатия <ENTER>}

ReadLn;

{Выход из графического режима в символьный}

CloseGraph;

End.


Графические примитивы. Хотя любое изображение можно построить из точек, но программировать получение сложного рисунка или чертежа, используя только процедуру поставить точку, было бы слишком неудобно и громоздко. В любом графическом пакете существуют процедуры рисования основных геометрических фигур: прямых линий, окружностей, эллипсов, прямоугольников и т. п. Такие фигуры называют графическими примитивами.

Рассмотрим несколько основных процедур рисования графических примитивов, имеющихся в модуле Graph.

Линия с заданными координатами концов (X1, Y1) и (Х2, Y2):


Procedure Line(X1,Y1,X2,Y2: Integer);


Линия от текущей точки до точки с координатами X, Y:


Procedure LineTo(X,Y: Integer);


Линия от текущей точки до точки с заданными приращениями координат DX, DY:


Procedure LineRel(DX,DY: Integer);


Прямоугольник с заданными координатами верхнего левого угла (X1, Y1) и нижнего правого угла (Х2, Y2):


Procedure Rectangle(XI,Y1,X2,Y2: Integer);


Окружность с центром в точке (X, Y) и радиусом R— в пикселях:


Procedure Circle(X,Y: Integer; R: Word);


Дуга окружности с центром в точке (X, Y), радиусом R, начальным углом BegA и конечным углом EndA. Углы измеряются в градусах против часовой стрелки от направления оси X.


Procedure Arc(X,Y: Integer; BegA,EndA,R: Word);


Эллипсная дуга с центром в точке X, Y с начальным и конечным углами BegA и EndA, горизонтальным радиусом RX и вертикальным радиусом RY:


Procedure Ellipse(X,Y: Integer; BegA,EndA,RX,RY: Word) ;


Пример 2. Составим программу, рисующую голову робота (рис. 32).



Рисунок содержит два прямоугольника, две окружности, две дуги, эллипс, три прямые линии и две красные точки. Заранее определяются все координаты и размеры элементов рисунка.


Uses Graph;

Var Driver,Mode: Integer;

Begin

{Инициализация графического режима}

Driver:=Detect;

InitGraph(Driver, Mode,'C:\TP\BGI');

SetColor(White);{белый цвет рисунка}

SetBkColor(Black);{черный цвет фона)

Rectangle(100,100,300,300);{голова}

Circle(150,170,30);(левый глаз}

Circle(250,170,30);{правый глаз}

Arc(150,170,45,135,40);{левая бровь}

Arc(250,170,45,135,40);{правая бровь}

Ellipse(200,250,0,359,10,20);{нос}

Rectangle(130,280,270,290);{рот}

MoveTo(100,300);{установка вниз влево}

LineTo(50,350);{три}

LineTo(350,350);{линии}

LineTo(300,300);{шеи}

PutPixel(150,170,Red);{левый зрачок}

PutPixel(250,170,Red);{правый зрачок}

ReadLn;{задержка}

CloseGraph;(выход из графики}

End.


В приведенном примере все линии рисуются сплошными и стандартной толщины. Модуль Graph позволяет управлять стилем линии (сплошная, пунктирная, точечная и т.п.) и толщиной. Для этого существует процедура SetLineStile (см. приложение 2).

Закраски и заполнения. Среди графических примитивов существуют закрашенные области. Цвет закраски определяется процедурой SetColor. Кроме того, можно управлять рисунком закраски (типом заполнения). Это может быть сплошная закраска, заполнение редкими точками, крестиками, штрихами и т.п. В табл. П2.3 приложения 2 описаны константы для указания типа заполнения.

Процедура определения типа заполнения (Fill) и цвета заполнения (Color) имеет следующий заголовок:


Procedure SetFillStyle(Fill,Color: Word);


Заполненная прямоугольная область с заданными координатами углов:


Procedure Bar(XI,Y1,X2,Y2: Integer);


Обведенный линией (SetLineColor, SetLineStyle) и закрашенный (SetFillStyle) эллипс:


Procedure FillEllips(X,Y,RX,RY: Integer);


Обведенный линией и закрашенный эллипсный сектор:


Procedure Sector(X,Y: Integer;

BegA,EndA,RX,RY: Word);


Обведенный линией и закрашенный сектор окружности:


Procedure PieSlice(X,Y:Integer;

BegA,EndA: Word);


Наконец, можно закрасить любую область, ограниченную замкнутой линией. Для этого нужно указать какую-нибудь точку внутри этой области (X, Y) и цвет граничной линии (Border). Соответствующая процедура выглядит следующим образом:


Procedure FloodFill(X,Y: Integer; Border: Word);


Модуль Graph позволяет выводить на графический экран тексты. Мы не будем сейчас детально обсуждать эту проблему, необходимую информацию можно найти в соответствующей литературе. Приведем лишь пример одной текстовой процедуры, с помощью которой выводится в графическое окно символьная строка (Txt), начиная с указанной позиции (X,Y).


Procedure OutTextXY(X,Y: Integer; Txt: String);


Например, чтобы вывести под нашим рисунком строку «ЭТО РОБОТ», следует в программу добавить оператор


OutTextXY(195,400,'ЭТО РОБОТ')

Вместе с графиком функции строятся оси координат. Ось Х имеет координату Yg= 90, ось Y — координату Xg = 10.


Uses Graph;

Var Driver,Mode: Integer;

X: Real; Xg,Yg,I: Integer;

Begin

{Инициализация графического режима)

Driver:=Detect;

InitGraph(Driver,Mode,'C:\TP\BGI');

SetColor(White);{белый цвет линий)

SetBkColor(Black);{черный цвет фона)

Line(10,90,200,90);{ось Х)

Line(10,20,10,160);{ось Y)

{Построение графика функции желтыми точками)

Х:=0;

For I:=0 То 190 Do

Begin Xg:=10+Round(95/Pi*X);

Yg:=90-Round(50*Sin(X));

PutPixel(Xg,Yg,Yellow);

X:=X+Pi/95

End;

{Разметка осей, запись функции)

OutTextXY(15,30,'Y');

OutTextXY(205,90,'X');

OutTextXY(130,40,'Y=SIN(X)');

ReadLn;(задержка)

CloseGraph; {выход из графики)

End.


Упражнения


1. Составить программу «Звездное небо»: в черном окне случайным образом появляются белые точки. Работа программы заканчивается по нажатию клавиши.

2. Изменить программу «Звездное небо» так, чтобы наряду с зажиганием новых звезд происходило угасание (закрашивание цветом фона) уже светящихся звезд.

3. В программу «Робот» внести такие изменения, в результате которых робот окажется раскрашенным в разные цвета.

4. Используя линии и другие графические примитивы, составить программу, рисующую дом.

5. Составить программу рисования на экране шахматного поля.

6. Написать универсальную процедуру построения графика функции у = F(x) точечным методом. Процедура должна иметь следующие Параметры: Xmin, Xmax, Ymin, Ymax, Xgmin, Xgmax, Ygmin, Ygmax. Функция F(x) описывается во внешней подпрограмме-функции.

7. Исследовав область определения и выбрав расположение координатных осей, построить на экране графики функций:




используя процедуру из предыдущей задачи.

Строковый тип данных


Теперь мы познакомимся с типом данных, который относится к числу структурированных. Это строковый тип данных (строка). Следует заметить, что строковый тип данных есть в Турбо Паскале и отсутствует в стандартном Паскале.

Строка — это последовательность символов. Каждый символ занимает 1 байт памяти (код ASCII). Количество символов в строке называется ее длиной. Длина строки может находиться в диапазоне от 0 до 255. Строковые величины могут быть константами и переменными.

Строковая константа есть последовательность символов, заключенная в апострофы. Например:


'Язык программирования ПАСКАЛЬ',

'IBM PC — computer',

'33-45-12'.


Строковая переменная описывается в разделе описания переменных следующим образом:


Var <идентификатор>: String[<максимальная длина строки>]


Например:


Var Name: String[20]


Параметр длины может и не указываться в описании. В таком случае подразумевается, что он равен максимальной величине — 255. Например:


Var slovo: String


Строковая переменная занимает в памяти на 1 байт больше, чем указанная в описании длина. Дело в том, что один (нулевой) байт содержит значение текущей длины строки. Если строковой переменной не присвоено никакого значения, то ее текущая длина равна нулю. По мере заполнения строки символами ее текущая длина возрастает, но она не должна превышать максимальной по описанию величины.

Символы внутри строки индексируются (нумеруются) от единицы. Каждый отдельный символ идентифицируется именем строки с индексом, заключенным в квадратные скобки. Например:


Name[5], Name[i], slovo[k+1].


Индекс может быть положительной константой, переменной, выражением целого типа. Значение индекса не должно выходить за границы описания.

Тип String и стандартный тип char совместимы. Строки и символы могут употребляться в одних и тех же выражениях.

Строковые выражения строятся из строковых констант, переменных, функций и знаков операций. Над строковыми данными допустимы операции сцепления и операции отношения.

Операция сцепления (+) применяется для соединения нескольких строк в одну результирующую строку. Сцеплять можно как строковые константы, так и переменные.

Например:


'ЭВМ'+'IВМ'+'РС'.


В результате получится строка:


'ЭВМ IBM PC'.


Длина результирующей строки не должна превышать 255. Операции отношения =, <

, >, <=, >=, <> производят сравнение двух строк, в результате чего получается логическая величина (true или false). Операция отношения имеет более низкий приоритет, чем операция сцепления. Сравнение строк производится слева направо до первого несовпадающего символа, и больше считается та строка, в которой первый несовпадающий символ имеет больший номер в таблице символьной кодировки.

Если строки имеют различную длину, но в общей части символы совпадают, считается, что более короткая строка меньше, чем более длинная. Строки равны, если они полностью совпадают по длине и содержат одни и те же символы.

Пример:

Выражение Результат

'cosmi'<'cosm2' True

'pascal'>'PASCAL' True

'Ключ_'<>'Ключ' True

'MS DOS'='MS DOS' True


Функция Copy (S, Poz, N) выделяет из строки s подстроку длиной в N символов, начиная с позиции Poz.N и Poz — целочисленные выражения.

Пример:

Значение S Выражение Результат

'ABCDEFG' Copy(S,2,3) 'BCD'

'ABCDEFG' Copy(S,4,4) 'DEFG'


Функция Concat (Sl, S2, ..., SN) выполняет сцепление (конкатенацию) строк S1,... ,SN в одну строку.

Пример:

Выражение Результат

Concat('АА','XX','Y') 'AAXXY'


Функция Length (S) определяет текущую длину строки S. Результат — значение целого типа.

Пример:

Значение S Выражение Результат

'test-5' Length(S) 6

'(А+В)*С' Length(S) 7


Функция Pos (Sl, S2) обнаруживает первое появление в строке S2 подстроки Sl. Результат — целое число, равное номеру позиции, где находится первый символ подстроки S1.

Если в строке S2 подстроки Sl не обнаружено, то результат равен 0.

Пример:

Значение S2 Выражение Результат

'abcdef Pos('cd',S2) 3

'abcdcdef Pos('cd',S2) 3

'abcdef Pos('k',S2) 0


Процедура Delete (S, Poz, N) выполняет удаление N символов из строки S, начиная с позиции Poz.

Пример:

Исходное значение S Оператор Конечное значение S

'abcdefg' Delete(S,3,2) 'abefg'

'abcdefg' Delete (S,2,6) 'a'


В результате выполнения процедуры уменьшается текущая длина строки в переменной S.

Процедура Insert(Sl,S2,Poz) выполняет вставку строки S1 в строку S2, начиная с позиции Poz.

От исходной символьной информации он должен перейти к работе с числовой информацией. Если предположить, что строка составлена только из четырех символов в соответствии с указанным форматом, то задача решается довольно просто. Вот программа такого интерпретатора:


Program Interpretator;

Var Str: String[4];

А, В: 0..9;

С: -100..100;

Begin

{ввод исходной строки}

WriteLn('Введите выражение!');

WriteLn;

Read(Str);

{преобразование цифровых символов в числа}

A:=Ord(Str[l])-Ord('0');

B:=Ord(Str[3])-Ord('0');

(выполнение арифметической операции)

Case Str[2] Of

'+': С:=А+В;

'-': С:=А-В;

'*': С:=А*В

End;

{вывод результата}

WriteLn(С:2)

End.


В этой программе появился новый для нас оператор. Он называется оператором выбора. Формат этого оператора описывается синтаксической диаграммой (рис. 33).






Здесь <селектор> — это выражение любого порядкового типа; <константа> — постоянная величина того же типа, что и селектор; <оператор> — любой простой или составной оператор.

Выполнение оператора выбора происходит так: вычисляется выражение-селектор; затем в списках констант ищется такое значение, которое совпадает с полученным значением селектора; далее исполняется оператор, помеченный данной константой. Если такой константы не найдено, то происходит переход к выполнению оператора, следующего после оператора выбора.

В приведенной выше программе роль селектора играет символьная величина Str[2]. Если она равна +, то выполнится оператор c:=a+b; если равна -, то выполнится оператор с:=а-b; если равна *, выполнится оператор с:=а*b. Для любых других значений Str[2] не выполнится ни один из операторов присваивания, и значение переменной С останется неопределенным.

Приведенное выше описание оператора выбора соответствует стандарту Паскаля. В Турбо Паскале допустимо использование в операторе Case альтернативной ветви после служебного слова Else. Вот пример для той же задачи. Если мы хотим, что-. бы в случае неверного символа в Str[2] выдавалось сообщение об этом, нужно программировать так:


Case Str[2] Of

'+': С:=А+В;

'-': С:=А-В;

'*': С:=А*В

Else WriteLn("неверный знак операции')

End;


А теперь вернемся к программе interpretator и разберемся в том, как она будет выполняться.

После ввода строки цифровые символы переводятся в соответствующие десятичные числа. Затем интерпретируется знак операции. В зависимости от знака выполняется одно из трех арифметических действий. Далее результат выводится на экран после символа =.


Упражнения


1. Составить программу получения из слова «дисковод» слова «воск», используя операцию сцепления и функцию Copy.

2. Составить программу получения слова «правило» из слова «операция», используя процедуры Delete, Insert.

3. В данном слове заменить первый и последний символы на *.

4. В данном слове произвести обмен первого и последнего символов.

5. К данному слову присоединить столько !, сколько в нем имеется букв (например, из строки «УРА» получить «УРА!!!»).

6. В данной строке вставить пробел после каждого символа.

7. Удвоить все буквы во введенном слове.

8. Перевернуть введенную строку (например, из «ДИСК» получится «КСИД»).

9. В данной строке удалить все пробелы.

10. Строка представляет собой запись целого числа. Составить программу перевода ее в соответствующую величину целого типа.

Табличные данные и массивы


В повседневной и научной практике часто приходится встречаться с информацией, представленной в табличной форме. Вот, например, таблица, содержащая среднемесячные значения температуры, °С, за определенный год:






Такую таблицу называют линейной. Она представляет собой последовательность упорядоченных чисел. Если требуется какая-то математическая обработка этих данных, то для их обозначения обычно вводят индексную символику. Например, через Т1 обозначается температура января (первого месяца), Т5 — температура мая и т. д. В общем виде множество значений, содержащихся в таблице, обозначается так:


{Тi}, i=1,...,12.

Тип элементов массива называется его базовым типом. Очевидно, что для рассмотренных массивов температур базовым типом является вещественный (Real).

Описание массивов. Переменная регулярного типа описывается в разделе описания переменных в следующей форме:


Var <идентификатор>: Array[<тип индекса>] Of <тип компонент>


Чаще всего в качестве типа индекса употребляется интервальный тип. Например, рассмотренный выше одномерный массив среднемесячных температур опишется так:


Var Т: Array[1..12] Of Real;


Описание массива определяет, во-первых, размещение массива в памяти, во-вторых, правила его дальнейшего употребления в программе. Последовательные элементы массива располагаются в последовательных ячейках памяти (T[1], T[2] и т. д.), причем значения индекса не должны выходить из диапазона 1... 12. В качестве индекса может употребляться любое выражение соответствующего типа. Например, Т[i+j], Т[m div 2].

Тип индекса может быть любым скалярным порядковым типом, кроме integer. Например, в программе могут присутствовать следующие описания:


Var Cod: Array[Char] Of 1..100;

L: Array[Boolean] Of Char;


В такой программе допустимы следующие обозначения элементов массивов:


cod['x']; L[true]; cod[chr (65) ]; L[a>0]


В некоторых случаях бывает удобно в качестве индекса использовать перечисляемый тип. Например, данные о количестве учеников в четырех десятых классах одной школы могут храниться в следующем массиве:


Type Index=(А,В,С,D);

Var Class_10: Array[Index] Of Byte;


И если, например, элемент Class_l0[A] равен 35, то это означает, что в 10«А» классе 35 чел. Такое индексирование улучшает наглядность программы.

Часто структурированному типу присваивается имя в разделе типов, которое затем используется в разделе описания переменных.


Type Mas1=Array[1..100] Of Integer;

Mas2=Array [-10..10] Of Char;

Var Num: Mas1; Sim: Mas2;


До сих пор речь шла об одномерных массивах, в которых типы элементов скалярные.

Многомерный массив в Паскале трактуется как одномерный массив, тип элементов которого также является массивом (массив массивов). Например, рассмотренную выше прямоугольную таблицу можно хранить в массиве, описанном следующим образом:

Var H: Аггау[1981..1990]. Of Array[1..12] Of Real;


Вот примеры обозначения некоторых элементов этого массива:


Н[1981][1]; Н[1985][10]; Н[1990][12]


Однако чаще употребляется другая, эквивалентная форма обозначения элементов двумерного массива:


Н[1981,1]; Н[1985,10]; Н[1990,12]

Переменная H[1981] обозначает всю первую строку таблицы, т.е. весь массив температур за 1981 г.

Другим вариантом, эквивалентным приведенному выше описанию, является следующий:


Type Month=Array[1..12] Of Real;

Year=Array [1981..1990] Of Month;

Var H: Year;


Наиболее краткий вариант описания данного массива такой:


Var H: Array[1981..1990,1..12] Of Real;


Продолжая по аналогии, можно определить трехмерный массив как одномерный массив, у которого элементами являются двумерные массивы. Вот пример описания трехмерного массива:


Var A: Array[l..10,1..20,1..30] Of Integer;


Это массив, состоящий из 10 • 20 • 30 = 6000 целых чисел и занимающий в памяти 6000 • 2 = 12000 байт. В Паскале нет ограничения сверху на размерность массива. Однако в каждой конкретной реализации Паскаля ограничивается объем памяти, выделяемый под массивы. В Турбо Паскале это ограничение составляет 64 килобайта.

По аналогии с математикой одномерные числовые массивы часто называют векторами, а двумерные — матрицами.

В Паскале не допускается употребление динамических массивов, т.е. таких, размер которых определяется в процессе выполнения. Изменение размеров массива происходит через изменение в тексте программы и повторную компиляцию. Для упрощения таких изменений удобно определять индексные параметры в разделе констант:


Const Imax=10; Jmax=20;

Var Mas: Array[1..Imax,1..Jmax] Of Integer;


Теперь для изменения размеров массива Mas и всех операторов программы, связанных с этими размерами, достаточно отредактировать только одну строку в программе — раздел констант.

Действия над массивом как единым целым. Такие действия допустимы лишь в двух случаях:

• присваивание значений одного массива другому;

• операции отношения «равно», «не равно».

В обоих случаях массивы должны иметь одинаковые типы (тип индексов и тип элементов).

Пример:


Var P,Q: Array[1..5,1..10] Of Real;


При выполнении операции присваивания P:=Q все элементы массива P станут равны соответствующим элементам массива Q.

Как уже отмечалось, в многомерных массивах переменная с индексом может обозначать целый массив

Например, если в таблице H требуется, чтобы данные за 1989 г. были такими же, как за 1981 г. (девятой строке присвоить значение первой строки), то это можно делать так:


Н[1989]:=Н[1981]


А если нужно поменять местами значения этих строк, то это делается через третью переменную того же типа:


Р:=Н[1989];Н[1989]:=Н[1981];Н[1981]:=Р;


где Р oписана так:


Var Р: Array[1..12] Of Real;


Обработка массивов в программах производится покомпонентно. Вот примеры ввода значений в массивы:


For I:=l То 12 Do

ReadLn(T[l]);

For I:=l To IMax Do

For J:=l To JMax Do

ReadLn(Mas[I,J]);


Здесь каждое следующее значение будет вводиться с новой строки. Для построчного ввода используется оператор Read.

Аналогично в цикле по индексной переменной организуется вывод значений массива. Например:


For I:=l То 12 Do Write(Т[I]:8:4);


Следующий фрагмент программы организует построчный вывод матрицы на экран:


For I:=1 То IMax Do

Begin

For J:=l To JMax Do

Write(Mas[I,J]:6);

WriteLn

End;


После печати очередной строки матрицы оператор WriteLn без параметров переведет курсор в начало новой строки. Следует заметить, что в последнем примере матрица на экране будет получена в естественной форме прямоугольной таблицы, если JMax не превышает 12 (сами подумайте почему).

Рассмотрим несколько примеров типовых программ обработки массивов.

Пример 1. Вернемся к массиву среднемесячных температур T[1.. 12]. Требуется вычислить среднегодовую температуру, а также ежемесячные отклонения от этой величины.


Program Example;

Const N = 12;

Type Vec=Array [1..N] Of Real;

Var T,Dt: Vec;

St: Real;

I: Integer;

Begin (Ввод исходных данных)

WriteLn('Вводите таблицу температур');

For I:=l To N Do

Begin

Write(I: 2,':');

ReadLn(T[I])

End;

{Вычисление средней температуры}

St:=0;

For I:=1 To N Do

St:=St+T[I];

St:=St/N;

(Вычисление таблицы отклонений от среднего}

For I:=1 To N Do

Dt[I]:=T[I]-St;

{Вывод результатов}

WriteLn('Средняя температура равна',St:6:2);

WriteLn;

WriteLn('Отклонения от средней температуры:');

For I:=l To N Do

WriteLn(1:1,':',Dt[I]:6:2)

End.


По этой программе можно рассчитать среднее значение и вектор отклонений от среднего для любого одномерного вещественного массива. Настройка на размер массива осуществляется только редактированием раздела констант.

Пример 2. Выбор максимального элемента

Пусть из рассмотренного выше массива температур требуется отобрать самую высокую температуру и номер месяца, ей соответствующего. Идея алгоритма решения этой задачи: чтобы получить максимальную температуру в вещественной переменной TMах, сначала в нее заносится первое значение массива T[1]. Затем поочередно сравнивается значение TMах с остальными элементами массива температур, и каждое значение большее, чем TMах, присваивается этой переменной. Для получения номера самого теплого месяца в целой переменной NumMax в нее следует каждый раз засылать номер элемента массива температур одновременно с занесением в TMах его значения.


ТМах:=Т[1];

NumMax:=1;

For I:=2 To 12 Do

If T[I]>Tmax

Then

Begin

TMax:=T[I];

NumMax:=1

End;


Заметим, что если в массиве температур несколько значений, равных максимальному, то в NumMax будет получен первый номер из этих элементов. Чтобы получить последнюю дату, нужно в операторе If заменить знак отношения > на >=.

Пример 3. Сортировка массива. В одномерном массиве Х из N элементов требуется произвести перестановку значений так, чтобы они расположились по возрастанию, т.е. Х1 ≤ Х2 ≤... ≤ ХN.

Существует целый класс алгоритмов сортировки. Ниже описан алгоритм, который называется «метод пузырька».

Идея: производится последовательное упорядочивание смежных пар элементов массива: Х1 и X2, Х2 и Х3,.... ХN-1 и ХN. В итоге максимальное значение переместится в ХN. Затем ту же процедуру повторяют до XN-1 и т.д., вплоть до цепочки из двух элементов Х1 и X2. Такой алгоритм будет иметь структуру двух вложенных циклов с внутренним циклом — переменной (сокращающейся) длины.


For I:=1 То N-l Do

For K:=l To N-I Do

If Х[К]>Х [K+l]

Then

Begin

А:=Х[К];

Х[К]:=Х[К+1];

Х[К+1]:=А

End;


Пример 4. Дан описанный выше двумерный массив среднемесячных температур за 10 лет. Определить, в каком году было самое теплое лето, т. е. в каком году была наибольшая средняя температура летних месяцев.

Идея решения: в векторе S получить средние температуры летних месяцев за 10 лет. Затем найти номер наибольшего элемента в этом векторе, это и будет искомый год.


Program Example_2;

Type Month=Array[l..12] Of Real;

Year=Array[1981..1990] Of Month;

Var H: Year;

S: Array[1981..1990] Of Real;

I,J,K: Integer;

Begin {Ввод данных с клавиатуры)

For I:=1981 То 1990 Do

For J:=l To 12 Do

Begin

Write(J:2,'.',I:4,':');

ReadLn(H[I,J])

End;

{Вычисление вектора средних летних температур}

For I:=1981 To 1990 Do

Begin S[I]:=0;

For J: =6 To 8 Do

S[I]:=S[I]+H[I,J];

S[I]:=S[I]/3

End;

{Определение года с самым теплым летом}

К:=1981;

For I:=1982 То 1990 Do

If S[I]>S[K] Then K:=I;

WriteLn('Самое теплое лето было в', К,'-м году')

End.

Упражнения:

3. Для вектора {хi}, i = 1,..., 20, подсчитать количество компонент, значения которых лежат в интервале [0,1].

4. Даны два вектора {хi}, {уi}, i = 1,..., 10, упорядоченные по возрастанию. Слить их в один вектор {zi}, i = 1, …, 20, так чтобы сохранилась упорядоченность.

5. Дан массив, состоящий из 100 целых чисел. Вывести все числа, которые встречаются в этом массиве:

а) несколько раз;

б) только по одному разу.

6. В целочисленной матрице размером 10 х 10 найти значение и индексы максимального элемента.

7. В двоичной матрице 5 х 10 определить номер строки с наибольшим количеством нулей.

8. Все строки вещественной матрицы 10 х 15 упорядочить по убыванию значений их элементов.

9. Транспонировать целочисленную матрицу 5 х 5, т.е. отразить относительно главной диагонали.

10. В двоичной матрице 10 х 10 найти совпадающие строки.

Понятие множества. Множественный тип данных


Одним из фундаментальных разделов математики является теория множеств. Некоторые моменты математического аппарата этой теории реализованы в Паскале через множественный тип данных (множества).

Множеством называется совокупность однотипных элементов, рассматриваемых как единое целое. В Паскале могут быть только конечные множества. В Турбо Паскале множество может содержать от 0 до 255 элементов.

В отличие от элементов массива элементы множества не пронумерованы, не упорядочены. Каждый отдельный элемент множества не идентифицируется, и с ним нельзя выполнить какие-либо действия. Действия могут выполняться только над множеством в целом.

Тип элементов множества называется базовым типом. Базовый тип может быть любым скалярным, за исключением типа Real.

Конструктор множества. Конкретные значения множества задаются с помощью конструктора множества, представляющего собой список элементов, заключенный в квадратные скобки. Сами элементы могут быть либо константами, либо выражениями базового типа. Вот несколько примеров задания множеств с помощью конструктора:

[3,4,7,9,12] — множество из пяти целых чисел;

[1.. 100] — множество целых чисел от 1 до 100;

['a','b','c'] — множество, содержащее три литеры а, Ь, с;

['a'.,'z','?','!'] — множество, содержащее все прописные латинские буквы, а также знаки ? и !.

Символы [] обозначают пустое множество, т.е. множество, не содержащее никаких элементов.

Не имеет значения порядок записи элементов множества внутри конструктора. Например, [1,2,3] и [3,2,1] эквивалентные множества.

Каждый элемент в множестве учитывается только один раз. Поэтому множество [1,2,3,4,2,3,4,5] эквивалентно [1.. 5 ].

Переменные множественного типа описываются так:


Var <идентификатор>: Set Of <базовый тип>


Например:


Var A,D: Set Of Byte;

В: Set Of ' a' . . ' z;

C: Set Of Boolean;


Нельзя вводить значения во множественную переменную оператором ввода и выводить оператором вывода. Множественная переменная может получить конкретное значение только в результате выполнения оператора присваивания следующего формата:


<множественная переменная>: <множественное выражение>


Например:


А:=[50,100,150,200];

B:=['m', 'n','k'];

С:=[True,False] ;

D:=A;


Кроме того, выражения могут включать в себя операции над множествами.

Операции над множествами. В Паскале реализованы основные операции теории множеств. Это объединение, пересечение, разность множеств. Во всех таких операциях операнды и результаты есть множественные величины одинакового базового типа.

Объединение множеств. Объединением двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В. Знак операции объединения в Паскале +.

На рис. 34, а схематически показан результат объединения двух множеств.

Например:


[1,2,3,4]+[3,4,5,6]→[1,2,3,4,5,6]


Пересечение множеств. Пересечением двух множеств А и В называется множество, состоящее из всех элементов принадлежащих, одновременно множеству А и множеству В (см. рис. 34, б) Знак операции пересечения в Паскале *.

Например:


[1,2,3,4]*[3,4,5,6]→[3,4]


Разность множеств. Разностью двух множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Например:


[1,2,3,4]-[3,4,5,6]→[1,2]

[3,4,5,6]-[1,2,3,4]→[5,6]

Пример 1. Дана символьная строка. Подсчитать в ней количество знаков препинания (. - , ; : ! * ?).


Program P1;

Var S: String; I,K: Byte;

Begin

ReadLn(S); K:=0;

For I:=1 To Length(S) Do

If S[I] In ['.','-',',',';',':', '!', '*','?']

Then K:=K+1;

WriteLn('Число знаков препинания равно',К)

End.


В этом примере использована множественная константа с символьным типом элементов. Эту задачу можно решить и без множества, записав в операторе If длинное логическое выражение: (S[l]='.') Or (S[l]='-') и т.д. Использование множества сокращает запись.

Пример 2. Даны две символьные строки, содержащие только строчные латинские буквы. Построить строку S3, в которую войдут только общие символы S1 и S2 в алфавитном порядке и без повторений.


Program Р2;

Type Mset=Set Of 'a'..'z';

Var S1,S2,S3: String;

MS1,MS2,MS3: Mset;

C: Char;

Procedure SM(S: String; Var MS: Mset);

{Процедура формирует множество MS, содержащее все символы строки S}

Var I: Byte;

Begin MS:=[] ;

For I:=1 To Length(S) Do

MS:=MS+[S[I]]

End;

Begin {Ввод исходных строк)

ReadLn(S1);ReadLn(S2);

{Формирование множеств MS1 и MS2 из символов строк S1 и S2)

SM(S1,MS1);SM(S2,MS2);

{Пересечение множеств - выделение общих элементов в множество MS3}

MS3:=MS1*MS2;

{Формирование результирующей строки S3)

S3:=";

For С: ='а' То 'z' Do

If С In MS3 Then S3:=S3+C;

WriteLn('Результат:',S3)

End.


Пример 3. Составить программу, по которой из последовательности натуральных чисел от 2 до N (1 < N ≤ 255) будут выбраны все простые числа.

Для решения задач такого типа существует алгоритм, известный под названием «Решето Эратосфена». Суть его в следующем:

1. Из числовой последовательности выбираем минимальное значение, это будет простое число.

2. Удаляем из последовательности все числа, кратные выбранному.

3. Если после удаления последовательность не стала пустой, то возвращаемся к выполнению пункта 1.

Вот пример работы такого алгоритма для N = 15 (подчеркнуты выбранные простые числа):


2 3 4 5 6 7 8 9 10 11 12 13 14 15

3 5 7 9 11 13 15

5 7 11 13

7 11 13

11 13

13


Решение этой задачи удобно программировать, используя множественный тип.


Program Eratosfen;

Const N=201;

{Возможно любое значение 1<N<256}

Var А,В: Set Of 2..N;

K,P: Integer;

Begin

{Формирование исходного множества А; В - искомое множество простых чисел, сначала - пустое}

A:=[2..N]; В:=[]; Р:=2;

Repeat

{Поиск минимального числа в множестве А}

While Not(P In A) Do Р:=Р+1;

{Включение найденного числа в множество В)

В:=В+[Р];

К:=Р;

{Исключение из А чисел, кратных Р}

While K<=N Do

Begin

A:=A-[K];

K:=K+P;

End

Until A= [ ] ;

{Вывод результата, т.е. всех чисел из множества В в порядке возрастания}

For Р:=2 То N Do If P In В Then WriteLn(P)

End.


Красивая программа! К сожалению, ею нельзя воспользоваться для N > 255 из-за отмеченного выше ограничения на максимальный размер множества в Турбо Паскале.

Пример 4. Как уже говорилось, нельзя вводить значения непосредственно в множество. Однако такая потребность у программиста может возникнуть. В этом случае можно прибегнуть к процедуре INSET, описанной ниже. Для примера рассматривается множество с символьным базовым типом. Предполагается, что в основной программе глобально объявлен тип SetChar.


Type SetChar: Set Of Char;

Procedure INSET(Var M: SetChar);

Var I,N: Byte; C: Char;

Begin

Write('Укажите размер множества:'); ReadLn(N);

M:=[];

For I:=l To N Do

Begin

Write(1:1,'-и элемент:'); ReadLn(С);

M:=M+[C]

End;

WriteLn('Ввод завершен!')

End.


В основной программе для ввода значений в множество, например с именем sim, достаточно записать оператор: INSET (SIM);

Произойдет диалоговый ввод значений.


Упражнения


1. В программе присутствуют описания:

Var P: Set Of 0..9; I,J: Integer;


Если i = 3 и j = 5, то какое значение получит переменная Р при выполнении следующих операторов присваивания:


а) P:=[I+3,J Div 2,J..Sqr(I)-3];

б) P:=[2*I..J];

в) P:=[I,J,2*I,2*J]?


2. Вычислить значения отношений:


а)[2] <> [2, 2, 2]; б)['a','b']=['b','а'];

в)[4,5,6]=[4,5,6]; г)['с','b']=['с'..'Ь'];

д)[2, 3,5, 7] <=[!.. 9]; е)[3,6..8]<=[2..7,9];

ж)Тrunс(3.9)In[1,3,5]; з)Odd(4) In[].


3. Вычислить значения выражений:


а)[1,3,5]+[2,4]; б)[1,3,5]*[2,4];

в)[1,3,5]-[2,4]; г) [1..6]+[3..8];

д)[1..6]*[3..8]; е)[1..6]-[3..8];

ж)[]+[4]; з) []*[4];

и)[]-[4].


4. Составить программу подсчета количества различных значащих цифр в десятичной записи натурального числа.

5. Составить программу, печатающую в возрастающем порядке все целые числа из диапазона 1 ...255, представимые в виде n2+m2, где п, т > 0.

6. Дана строка из строчных русских букв. Между соседними словами — запятая, за последним словом — точка. Напечатать в алфавитном порядке:

а) все гласные буквы, которые входят в каждое слово;

б) все согласные буквы, которые не входят ни в одно слово;

в) все согласные буквы, которые входят только в одно слово;

г) все гласные буквы, которые входят более чем в одно слово.
 

Файлы. Файловые переменные


С термином «файл» вам уже приходилось встречаться. Прежде всего это понятие обычно связывают с информацией на устройствах внешней памяти. В Паскале понятие файла употребляется в двух смыслах:

• как поименованная информация на внешнем устройстве (внешний файл);

• как переменная файлового типа в Паскаль-программе (внутренний файл).

В программе между этими объектами устанавливается связь. Вследствие этого все, что происходит в процессе выполнения программы с внутренним файлом, дублируется во внешнем файле. С элементами файла можно выполнять только две операции: читать из файла и записывать в файл.

Файловый тип переменной — это структурированный тип, представляющий собой совокупность однотипных элементов, количество которых заранее (до исполнения программы) не определено.

Структура описания файловой переменной:


Var <имя переменной>: File Of <тип элемента>;


где <тип элемента> может быть любым, кроме файлового.

Например:


Var Fi: File Of Integer;

Fr: File Of Real;

Fc: File Of Char;

Пример 1. В файловую переменную Fx занести 20 вещественных чисел, последовательно вводимых с клавиатуры.
Var Fx: File Of Real;
X: Real; I: Byte;

Begin

Rewrite(Fx);

For I:=1 To 20 Do

Begin

Write ('?'); ReadLn(X);

Write(Fx,X)

End

End.


Для чтения элементов файла с его начала следует открыть файл для чтения. Это делает процедура Reset (FV).
Пример 2. В переменной х получить 10-й элемент вещественного файла Fx.


Program А;

Var Fx: File Of Real;

X: Real;

Begin

Reset(Fx) ;

For I:=l To 10 Do Read(Fx,X)

End.


Функция Eof (FV) проверяет маркер конца файла (end of file). Это логическая функция, которая получает значение true, если указатель установлен на маркер конца, в противном случае — false.

Пример 3. Просуммировать все числа из файла Fx, описанного в предыдущем примере.


Reset(Fx) ;

Sx:=0;

While Not Eof(Fx) Do

Begin

Read(Fx,X) ;

Sx:=Sx+X

End;


To же самое с помощью цикла Repeat можно делать следующим образом:


Repeat

Read(Fx,X);

Sx:=Sx+X

Until Eof(Fx);


Во втором варианте возможна ошибка чтения, если файл Fx пустой. Первый вариант от такой ошибки застрахован, поэтому он более предпочтителен.

Внешние файлы. В Турбо Паскале все внешние устройства (дисплей, клавиатура, принтер, диски и т.д.) трактуются как логические устройства с файловой структурой организации данных. Все немагнитные внешние устройства однофайловые. Иначе говоря, с каждым из них связан один файл со стандартным именем, предназначенный для обмена с внутренней памятью ЭВМ текстовой (символьной) информацией.

Стандартные имена логических устройств определяются операционной системой, в среде которой работает Паскаль. В системе MS DOS определены следующие имена:

CON (консоль) — логическое устройство, связанное при вводе с клавиатурой, при выводе — с экраном;

PRN (принтер) — логическое имя файла, связанного с устройством печати;

AUX — логическое имя коммуникационного канала, который используется для связи ПК с другими машинами;

INPUT — логическое имя стандартного устройства ввода, связанного с клавиатурой; при этом вводимые с клавиатуры символы отражаются на экране дисплея;

OUTPUT — логическое имя стандартного устройства вывода на экран.

Магнитный диск (МД) - многофайловое устройство. На нем хранятся как стандартные (системные) файлы, так и файлы, создаваемые пользователем. На магнитном диске могут создаваться файлы любых типов. Файлы на МД используются как в режиме чтения, так и в режиме записи.

Список файлов на диске хранится в директории (каталоге) диска. Каталог вызывается на экран системной командой DIR. В полной форме каталог содержит идентификаторы файлов, объем занимаемой памяти, дату и время создания файла. Идентификатор файла состоит из имени и типа файла:


<имя файла>.<тип файла>


Имя содержит от 1 до 8 латинских букв и (или) цифр; тип — необязательный элемент (от 0 до 3 символов), указывающий на характер информации, хранимой в файле.

Например:


PROGRAM. PAS — в файле текст программы на Паскале;

NUMBER. DAT — файл числовых данных;

NAMES. ТХТ — текстовый файл.


Для организации связи между файловой переменной и внешним файлом в Турбо Паскале используется процедура назначения:


Assign (<имя файловой переменной>,

<идентификатор внешнего файла>);


Здесь <идентификатор внешнего файла> — строковая величина (константа или переменная). Например:


Assign(Fi,'Number.dat');


После выполнения процедур Assign и Rewrite создается новый внешний файл, имя которого заносится в директорию.

Если файл открывается для чтения (Assign и Reset), то в указанном каталоге уже должен содержаться указанный внешний файл. В противном случае будет обнаружена ошибка.

Работа с файлом в программе завершается его закрытием с помощью процедуры


Close (<имя файловой, переменной>)


Например:


Close(Fi)


Подведем итог сказанному. Для создания и заполнения файла требуется следующая последовательность действий:

1. Описать файловую переменную.

2. Описать переменную того же типа, что и файл.

3. Произвести назначение (Assign).

4. Открыть файл для записи (Rewrite).

5. Записать в файл данные (Write).

6. Закрыть файл (Close).

Пример 4. Создать файл, содержащий среднесуточные температуры за некоторое количество дней. При этом необязательно предварительно указывать количество чисел во вводимой информации.

Можно договориться о каком-то условном значении, которое будет признаком конца ввода. Пусть, например, признаком конца ввода будет число 9999.


Program Taskl;

Var Ft: File Of Real; T: Real;

Begin

Assign(Ft,'Temp.dat'); Rewrite(Ft);

WriteLn('Вводите данные. Признак конца - 9999');

ReadLn(T);

While T<>9999 Do

Begin

Write(Ft,T); Write ('?'); ReadLn(T)

End;

WriteLn ('Ввод данных закончен");

Close(Ft)

End.


В результате работы этой программы на диске будет создан файл с именем Temp. dat, в котором сохранится введенная информация.

Для последовательного чтения данных из файла требуется выполнить следующие действия:

1. Описать файловую переменную.

2. Описать переменную того же типа.

3. Выполнить назначение (Assign).

4. Открыть файл для чтения (Reset).

5. В цикле читать из файла (Read).

6. Закрыть файл (Close).


Пример 5. Определить среднюю температуру для значений, хранящихся в файле Temp.dat.


Program Task2;

Var Ft: File Of Real;

T,St: Real; N: Integer;

Begin Assign(Ft,'Temp.dat');

Reset(Ft);

St:=0;

While Not Eof(Ft) Do

Begin

Read(Ft,T);

St:=St+T

End;

N:=FileSize(Ft);

St:=St/N;

WriteLn('Средняя температура зa',N:3,'суток равна',St:7:2,'гр-в');

Close(Ft)

End.


В этой программе использована функция определения размера файла:


FileSize (<имя файловой переменной>);


Ее результат — целое число, равное текущей длине файла.

Замечание: согласно стандарту Паскаля в файл, открытый оператором Rewrite, можно только записывать информацию, а файл, открытый оператором Reset, можно использовать только для чтения. В Турбо Паскале допускается запись (Write) в файл, открытый для чтения (Reset). Это создает определенные удобства для модификации файлов.

Текстовые файлы. Текстовый файл — наиболее часто употребляемая разновидность файлов. Как уже отмечалось раньше, немагнитные внешние устройства (логические) работают только с текстовыми файлами. Файлы, содержащие тексты программ на Паскале и других языках программирования, являются текстовыми. Различная документация, информация, передаваемая по каналам электронной связи, — все это текстовые файлы.

В программе файловая переменная текстового типа описывается следующим образом:


Var <идентификатор>:tехt;


Текстовый файл представляет собой символьную последовательность, разделенную на строки

Текстовый файл можно создать или преобразовать с помощью текстового редактора. Его можно просмотреть на экране дисплея или распечатать на принтере.

В программах на Паскале для работы с текстовыми файлами наряду с процедурами Read и Write употребляются процедуры ReadLn и WriteLn.


ReadLn(FV,<cписок ввода>)


Эта процедура читает строку из файла с именем FV, помещая прочитанное в переменные из списка ввода.


WriteLn(FV,<список вывода>)


Процедура записывает в файл FV значения из списка вывода, после чего выставляет маркер конца строки.

Для обнаружения конца строки в текстовом файле используется функция


Eoln(FV)


(End of line — конец строки). Это логическая функция, которая принимает значение true, если указатель файла достиг маркера конца строки и false — в противном случае.

Употребление операторов Read и ReadLn без указания имени файловой переменной обозначает чтение из стандартного файла Input (ввод с клавиатуры). Употребление операторов Write и WriteLn без имени файловой переменной обозначает запись в стандартный файл Output (вывод на экран). В таком варианте этими операторами мы уже многократно пользовались. Считается, что файлы INPUT и OUTPUT всегда открываются соответственно для чтения и записи при работе любой программы.

При вводе с клавиатуры маркер конца строки обнаруживается при нажатии на клавишу Enter.

Процедура ReadLn может использоваться без списка ввода. В этом случае происходит пропуск текущей строки в читаемом файле.

Употребление процедуры WriteLn без списка вывода обозначает вывод пустой строки (в файле выставляется маркер конца строки).

При записи в текстовый файл в списке вывода могут присутствовать форматы. Действия форматов мы уже рассматривали при обсуждении вывода данных на экран. Точно так же форматы работают и при выводе в текстовые файлы, связанные с любыми другими устройствами.

Пример 6. Пусть файл с именем Note.txt содержит некоторый текст. Требуется подсчитать количество строк в этом тексте.


Var Note: Text; К: Integer;

Begin Assign (Note,'Note.txt');

Reset(Note);

K:=0;

While Not Eof(Note) Do

Begin

ReadLn(Note); K:=K+1

End;

WriteLn ('Количество строк равно',К);

Close(Note)

End.


Используемый здесь оператор ReadLn (Note) «пролистывает» строки из текстового файла Note, не занося их в какую-либо переменную.

Пример 7. В текстовом файле Note.txt определить длину самой большой строки.


Var Note: Text;

Max,К: Integer; С: Char;

Begin

Assign(Note,'Note.txt');

Reset (Note);

Max:=0;

While Not Eof(Note) Do

Begin

K:=0;

While Not Eoln(Note) Do

Begin

Read(Note,C); K:=K+1

End;

If K>Max Then Max:=K;

ReadLn(Note)

End;

WriteLn('Наибольшая строка имеет', Max,'знаков');

Close(Note)

End.


Здесь каждая строчка прочитывается посимвольно, при этом в переменной к работает счетчик числа символов в строке. В переменной Мах отбирается наибольшее значение счетчика.

Упражнения


1. Дан файл вещественных чисел. Определить количество нулевых значений в этом файле.

2. Даны два файла целых чисел. Определить, являются ли они тождественными.

3. Даны два символьных файла одинакового размера. Произвести обмен информацией между ними.

4. Имеется внешний текстовый файл. Напечатать первую из самых коротких его строк.

5. Описать процедуру Lines(Т), которая построчно печатает содержимое непустого текстового файла Т, вставляя в начало каждой печатаемой строки ее порядковый номер (он должен занимать четыре позиции) и пробел.

6. В текстовом файле т записана непустая последовательность вещественных чисел, разделенных пробелами. Описать функцию Мах(Т) для нахождения наибольшего из этих чисел.

Комбинированный тип данных


Все структурированные типы данных, с которыми мы уже познакомились, представляют собой совокупности однотипных величин. Комбинированный тип данных — это структурированный тип, состоящий из фиксированного числа компонент (полей) разного типа. Комбинированный тип имеет еще и другое название — запись.

Такая структура называется двухуровневым деревом. В Паскале эта информация может храниться в одной переменной типа Record (запись). Задать тип и описать соответствующую переменную можно следующим образом:


Type Anketa1=Record

FIO: String[50]; {поля}

Pol: Char;

Dat: String[16]; {записи}

Adres: String[50];

Curs: 1..5; (или элементы)

Grup: 1..10;

Stip: Real {записи}

End;

Var Student: Anketa1;


Такая запись, так же как и соответствующее ей дерево, называется двухуровневой.

К каждому элементу записи можно обратиться, используя составное имя, которое имеет следующую структуру:


<имя переменной>.<имя поля>


Например, student. fio; student. dat и т.п. Если, например, требуется полю курс присвоить значение 3, то это делается так:


Student.Curs:=3 ;

Такая организация данных позволит, например, делать выборки информации по году рождения или по городу, где живут студенты. В этом случае описание соответствующей записи будет выглядеть так:


Type Anketa2=Record

FIO: String[50];

Pol: Char;

Dat: Record

God: Integer;

Mes: String[10];

Den: 1..31

End;

Adres: Record

Gorod: String[20];

UlDomKv: String[30];

End;

Curs: 1..5 ;

Grup: 1..10;

Stip: Real

End;

Var Student: Anketa2;


Поля такой записи, находящиеся на третьем уровне, идентифицируются тройным составным именем.

Например, student.Dat.God; student.Adres.Gorod.

Работа с файлами записей. Чаще всего записи используются как элементы файлов, составляющих компьютерные информационные системы. Рассмотрим примеры программ, работающих с файлами записей.

Пример 1. Сформировать файл FM.dat, содержащий экзаменационную ведомость одной студенческой группы. Записи файла состоят из следующих элементов: фамилия, имя, отчество; номер зачетной книжки; оценка.


Program Examen;

Type Stud=Record

FIO: String[30];

Nz: String[6];

Mark: 2..5

End;

Var Fstud: File Of Stud;

S: Stud;

N,I: Byte;

Begin

Assign(Fstud,'FM.DAT'); Rewrite(Fstud);

Write('Количество студентов в группе?');

ReadLn(N);

For I:=1 To N Do

Begin

Write(I:1,'-й,Фамилия И.О.'); ReadLn(S.FIO);

Write('Номер зачетки:'); ReadLn(S.Nz);

Write('Оценка:'); ReadLn(S.Mark);

Write(Fstud,S)

End;

WriteLn('Формирование файла закончено!');

Close(Fstud)

End.


Прежде чем перейти к следующему примеру, связанному с обработкой сформированного файла, рассмотрим еще одно средство работы с файлами, которое мы пока не обсуждали.

Прямой доступ к записям файла

В стандарте языка Паскаль допустим только последовательный доступ к элементам файла. Одной из дополнительных возможностей, реализованных в Турбо Паскале, является прямой доступ к записям файла.

Как уже отмечалось, элементы файла пронумерованы в порядке их занесения в файл, начиная с нуля. Задав номер элемента файла, можно непосредственно установить на него указатель. После этого можно читать или перезаписывать данный элемент. Установка указателя на нужный элемент файла производится процедурой


Seek(FV,n)


Здесь FV — имя файловой переменной, n — порядковый номер элемента. В следующем примере эта процедура будет использована.

Пример 2. Имеется файл, сформированный программой из предыдущего примера. Пусть некоторые студенты пересдали экзамен и получили новые оценки. Составить программу внесения результатов переэкзаменовки в файл. Программа будет запрашивать номер студента в ведомости и его новую оценку. Работа заканчивается, если вводится несуществующий номер (9999).


Program New_Marks;

Type Stud=Record

FIO: String[30];

Nz: String[6] ;

Mark: 2..5

End;

Var Fstud: File Of Stud;

S: Stud;

N: Integer;

Begin

Assign(Fstud,'FM.DAT');

Reset(Fstud) ;

Write('Номер в ведомости?');

ReadLn(N);

While N<>9999 Do

Begin

Seek(Fstud,N-l);

Read(Fstud,S);

Write(S.FIO,'оценка?');

ReadLn(S.Mark);

Seek(Fstud,N-l);

Write(Fstud,S);

Write('Номер в ведомости?');

ReadLn(N);

End;

WriteLn('Работа закончена!');

Close(Fstud)

End.


Пример требует некоторых пояснений. Список студентов в ведомости пронумерован, начиная от 1, а записи в файле нумеруются от 0. Поэтому, если n — это номер в ведомости, то номер соответствующей записи в файле равен n-1. После прочтения записи «номер n—1» указатель смещается к следующей n-й записи. Для повторного занесения на то же место исправленной записи повторяется установка указателя.


Упражнения


1. Описать запись, содержащую сведения о рейсе самолета.

2. Описать массив записей, содержащий таблицу Д.И.Менделеева. Составить программу заполнения массива.

3. Рассматривая комплексное число как двухэлементную запись, составить процедуры выполнения арифметических операций с комплексными числами.

4. Сведения о деталях, хранящихся на складе, содержат следующие атрибуты: название, количество, стоимость одной детали.

Составить программы, решающие следующие задачи:

а) заполнить файл с информацией о деталях на складе;

б) вычислить общую стоимость деталей;

в) выяснить, какие детали имеются в наибольшем количестве, какие — в наименьшем;

г) вывести информацию о наличии на складе деталей данного типа и их количестве;

д) внести изменения в файл после выдачи со склада определенного количества данного вида деталей. Если какой-то тип деталей полностью выбран со склада, то уничтожить запись о нем в файле.

Связаться со мной можно по электронной почте: anriasem@yandex.ru

  © Семенов Андрей Александрович, с. Стеклянное 2009-2015 г.